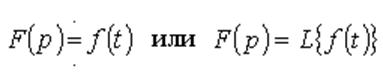
Следует отметить, что если оригинал ![]() увеличивается с
ростом t, то для сходимости интеграла (1) необходимо более быстрое убывание
модуля
увеличивается с
ростом t, то для сходимости интеграла (1) необходимо более быстрое убывание
модуля ![]() . Функции, с
которыми встречаются на практике при расчете переходных процессов, этому
условию удовлетворяют.
. Функции, с
которыми встречаются на практике при расчете переходных процессов, этому
условию удовлетворяют.
В качестве примера в табл. 1 приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.
Изображения типовых функций
|
Оригинал |
А |
|
|
|
|
|
|
Изображение |
|
|
|
|
|
|
Свойства изображений
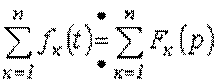 .
.
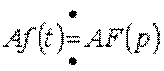 .
.
С использованием этих свойств и данных табл. 1, можно показать, например, что
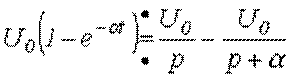 .
.
Изображения производной и интеграла
В курсе математики доказывается, что если 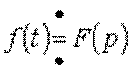 , то
, то 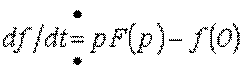 , где
, где ![]() - начальное значение функции
- начальное значение функции ![]() .
.
Таким образом, для напряжения на индуктивном элементе можно записать
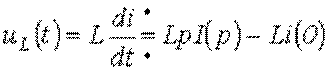
или при нулевых начальных условиях
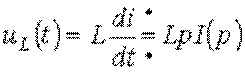 .
.
Отсюда операторное сопротивление катушки индуктивности
![]() .
.
Аналогично для интеграла: если 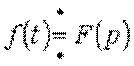 , то
, то 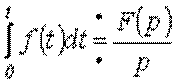 .
.
С учетом ненулевых начальных условий для напряжения на конденсаторе можно записать:
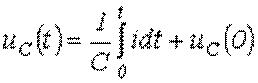 .
.
Тогда
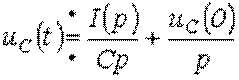
или при нулевых начальных условиях
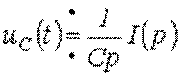 ,
,
откуда операторное сопротивление конденсатора
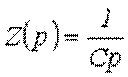 .
.
Закон Ома в операторной форме
Пусть имеем
некоторую ветвь ![]() (см. рис. 1),
выделенную из некоторой
(см. рис. 1),
выделенную из некоторой
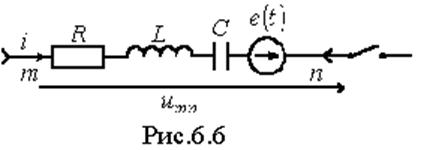
сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу, при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем случае ненулевые.
Для мгновенных значений переменных можно записать:
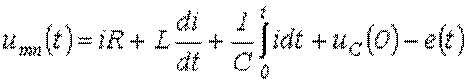 .
.
Тогда на основании приведенных выше соотношений получим:
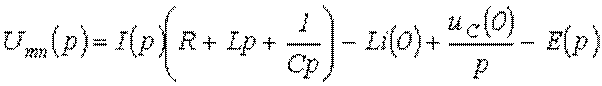 .
.
Отсюда
|
|
(2) |
где 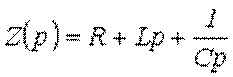 - операторное сопротивление рассматриваемого
участка цепи.
- операторное сопротивление рассматриваемого
участка цепи.
Следует обратить внимание, что операторное
сопротивление ![]() соответствует
комплексному сопротивлению
соответствует
комплексному сопротивлению ![]() ветви в цепи синусоидального тока при
замене оператора р на
ветви в цепи синусоидального тока при
замене оператора р на ![]() .
.
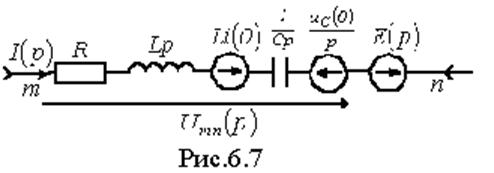
Уравнение (2) есть математическая запись закона Ома для участка цепи с источником ЭДС в операторной форме. В соответствии с ним для ветви на рис. 1 можно нарисовать операторную схему замещения, представленную на рис. 2.
Законы Кирхгофа в операторной форме
Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна нулю
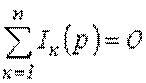 .
.
Второй закон Кирхгофа: алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура
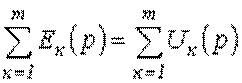 .
.
При записи уравнений по второму закону Кирхгофа следует помнить о необходимости учета ненулевых начальных условий (если они имеют место). С их учетом последнее соотношение может быть переписано в развернутом виде
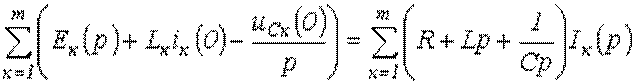 .
.
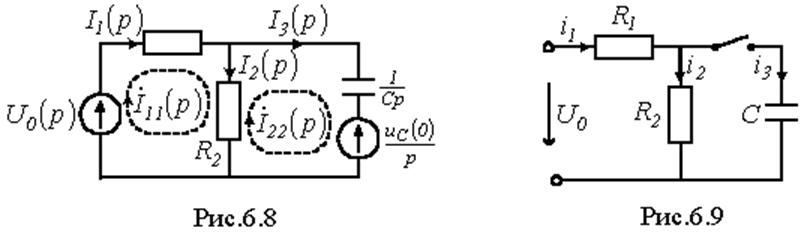
В качестве примера запишем выражение для
изображений токов в цепи на рис. 3 для двух
случаев: 1 - ![]() ; 2 -
; 2 - ![]() .
.
В первом случае в соответствии с законом Ома 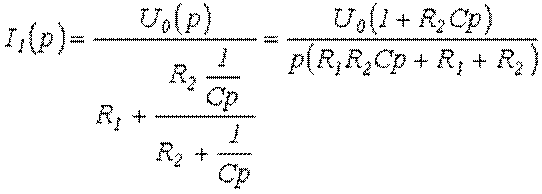 .
.
Тогда
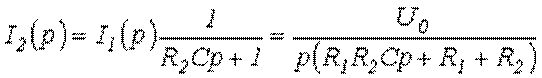
и
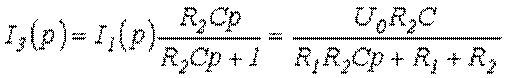 .
.
Во втором случае, т.е. при ![]() , для цепи на рис. 3 следует
составить операторную схему замещения, которая приведена на рис. 4. Изображения
токов в ней могут быть определены любым методом расчета линейных цепей,
например, методом контурных токов:
, для цепи на рис. 3 следует
составить операторную схему замещения, которая приведена на рис. 4. Изображения
токов в ней могут быть определены любым методом расчета линейных цепей,
например, методом контурных токов:
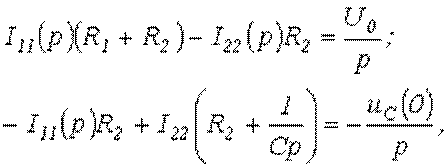
откуда ![]() ;
; ![]() и
и ![]() .
.
Переход от изображений к оригиналам
Переход от изображения искомой величины к оригиналу может быть осуществлен следующими способами:
1. Посредством обратного преобразования Лапласа
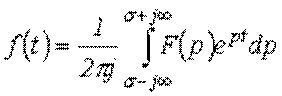 ,
,
которое представляет собой решение интегрального уравнения (1) и сокращенно записывается, как:
![]() .
.
На практике этот способ применяется редко.
2. По таблицам соответствия между оригиналами и изображениями
В специальной литературе имеется достаточно большое число формул соответствия, охватывающих практически все задачи электротехники. Согласно данному способу необходимо получить изображение искомой величины в виде, соответствующем табличному, после чего выписать из таблицы выражение оригинала.
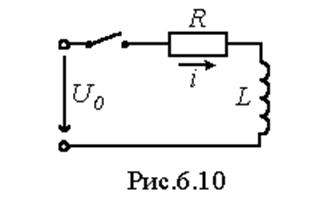 Например, для изображения тока в цепи на
рис. 5 можно записать
Например, для изображения тока в цепи на
рис. 5 можно записать
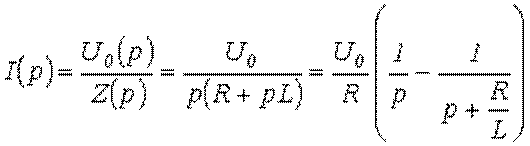 .
.
Тогда в соответствии с данными табл. 1
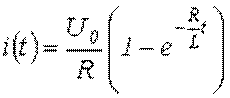 ,
,
что соответствует известному результату.
3. С использованием формулы разложения
Пусть изображение ![]() искомой переменной определяется
отношением двух полиномов
искомой переменной определяется
отношением двух полиномов
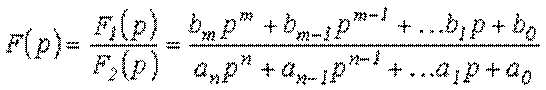 ,
,
где ![]() .
.
Это выражение может быть представлено в виде суммы простых дробей
|
|
(3) |
где ![]() - к-й корень уравнения
- к-й корень уравнения ![]() .
.
Для определения коэффициентов ![]() умножим левую и правую части
соотношения (3) на (
умножим левую и правую части
соотношения (3) на ( ![]() ):
):
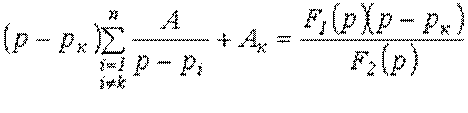 .
.
При ![]()
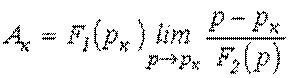 .
.
Рассматривая полученную неопределенность типа ![]() по правилу
Лапиталя, запишем
по правилу
Лапиталя, запишем
 .
.
Таким образом,
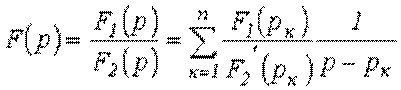 .
.
Поскольку отношение 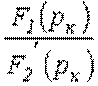 есть постоянный коэффициент, то
учитывая, что
есть постоянный коэффициент, то
учитывая, что  ,
окончательно получаем
,
окончательно получаем
|
|
(4) |
Соотношение (4) представляет собой формулу
разложения. Если один из корней уравнения ![]() равен нулю, т.е.
равен нулю, т.е. ![]() , то уравнение (4) сводится к виду
, то уравнение (4) сводится к виду
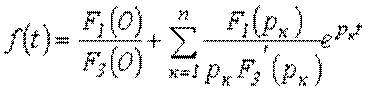 .
.
В заключение раздела отметим, что для нахождения
начального ![]() и
конечного
и
конечного ![]() значений
оригинала можно использовать предельные соотношения
значений
оригинала можно использовать предельные соотношения
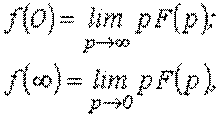
которые также могут служить для оценки правильности полученного изображения.
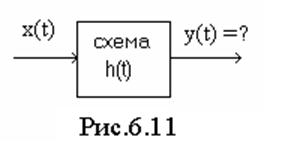 Он позволяет находить отклик цепи при нулевых
начальных условиях при произвольном входном сигнале и известной переходной
(импульсной) характеристики цепи (рис.6.6).
Он позволяет находить отклик цепи при нулевых
начальных условиях при произвольном входном сигнале и известной переходной
(импульсной) характеристики цепи (рис.6.6).
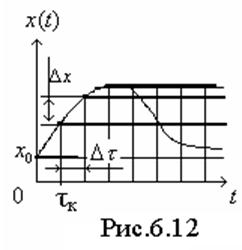 Произвольный импульсный сигнал (рис.6.7.) заменим совокупностью
элементарных ступенчатых сигналов с амплитудами ∆х, возникающими в моменты
времени τк со сдвигом по времени на
Произвольный импульсный сигнал (рис.6.7.) заменим совокупностью
элементарных ступенчатых сигналов с амплитудами ∆х, возникающими в моменты
времени τк со сдвигом по времени на ![]() .
.
Как следует из рисунка х0 - амплитуда
нулевого ступенчатого сигнала. Тогда отклик на него ![]() ;
;
![]() - амплитуда элементарного ступенчатого сигнала, рассчитывается
из выражения
- амплитуда элементарного ступенчатого сигнала, рассчитывается
из выражения ![]() , где х'(τк) –
производная от сигнала в момент времени τк,, она равна тангенса угла
наклона сигнала в момент времени τк. Тогда, отклик на элементарный
ступенчатый сигнал равен
, где х'(τк) –
производная от сигнала в момент времени τк,, она равна тангенса угла
наклона сигнала в момент времени τк. Тогда, отклик на элементарный
ступенчатый сигнал равен ![]() .
.
Используя принцип суперпозиции и переходя к пределу суммы при Δτ→0 (Δτ=dτ) можно записать что
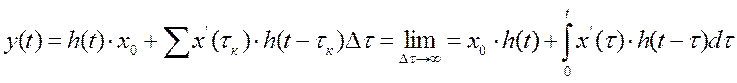 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.