Частотные характеристики и операторные функции электрических цепей, страница 10

Задачу будем решать классическим способом. За переменную в составляемом уравнении выбираем переменную, характеризующую энергетическое состояние цепи, которая наиболее просто связана с выходным сигналом. Такой переменной является напряжение на конденсаторе u_С(t) = u_2(t).

1)  Составим дифференцирующее уравнение относительно переменной состояния цепи и приведем его к стандартному виду.

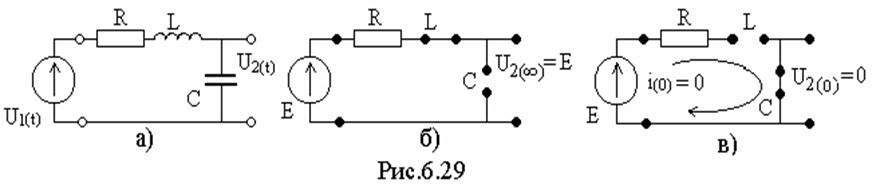
Данная цепь представляет контур, а потому используя, второй закон Кирхгофа и соотношения между напряжениям и токами на элементах схемы, запишем

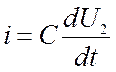,  отсюда , ;

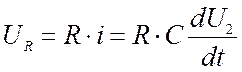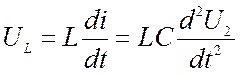Подставим полученные напряжения в первое выражение

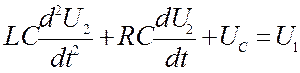
Поделим на LC, и введем обозначения 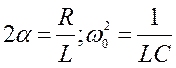 , получим

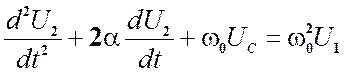
2)  Запишем общее решение.

Оно зависит от выходного сигнала, если выходной сигнал ступенчатый, то отклик записывается так:

 

3)  Найдем вынужденную составляющую общего решения - .

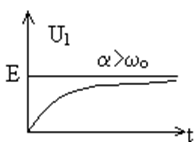
Для этого составим схему замещения исходной цепи при tà ∞,  (рис.6.24б), из которой и получим, что u_2(∞)=E.

4) Найдем показатели экспоненты - р₁ и p₂.

Коэффициенты  находят, как корни характеристического уравнения:

.

5) Найдем постоянные интегрирования А₁, А₂.

Их находят из начальных условий, т.е. при t=+0, для искомой функции, ее производных и послекоммутационной схемы (при t=+0, ωà∞), которая приведена на рис.6.24в.  Составим систему

,

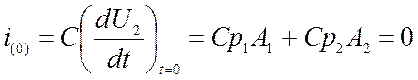из решения которой и находим А1 и А2

.

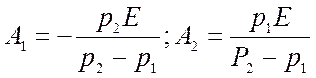6) Анализ корней и запись окончательного решения

а) если , то корни 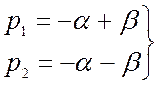- отрицательные действительные числа. И окончательное решение записывается так.

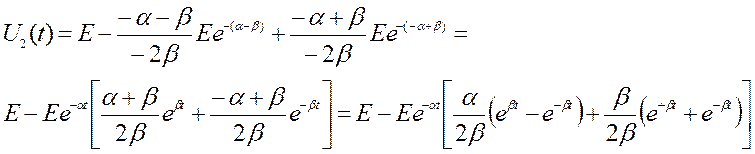
Учитывая, что 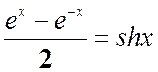;  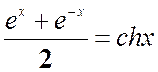, а также, что при βtà0,   окончательно получим

.

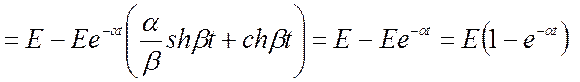Такое решение называется апериодическим

б) если , то корни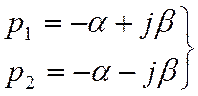 комплексно сопряженные числа. Если проделать то же самое, и учесть что

   ,

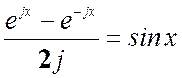
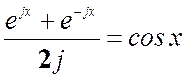то, при α << β, получим следующее

.

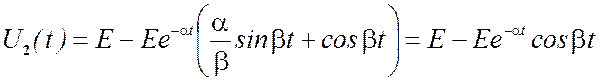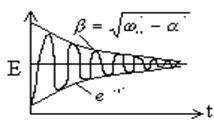Здесь ω₀ = (LC)^-1– собственная частота колебательного контура; β=(ω₀–α)^1/2  - частота собственных колебаний в контуре при наличии резистивных потерь; α= R/(2L) – скорость затухания собственных колебаний в контуре, α =1/τ, где τ= 2L/R – постоянная времени контура.

6.8. Связь между дифференциальным уравнением и характеристиками электрической цепи

1)  Для линейной цепи при произвольном входном сигнале х(t) связь между выходным и входным сигналом записывается в виде дифференциального уравнения.

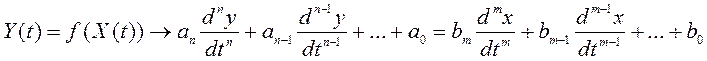
2) Связь дифференциального уравнения с частотной передаточной функцией. По определению частотная функция, есть H(jω)=.

Если входной сигнал гармонический

                                             (1)

если цепь линейная, то выходной сигнал обязательно гармонический

                                                (2)

Подставим 1 и 2 в дифференциальное уравнение

в результате получим

.

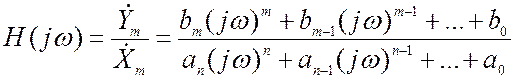2)  Связь частотной с операторной функцией цепи Н(р).

По определению Н(р) = H(jω)|_jω→p. Отсюда получаем

.

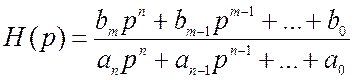4) Связь между импульсной и переходной характеристикой g(t) и h(t). Т.к. 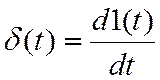,  то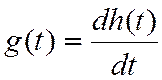

4)  Связь между g(t) и H(jω), H(p).

Из спектрального анализа следует выходной сигнал 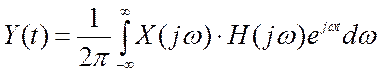. Если , то спектр ,

 следовательно 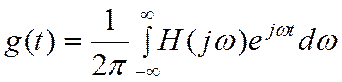: ОПФ

 следовательно 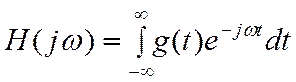: ППФ.

Таким образом, все способы описания электрической цепи связаны между собой.

Контрольные вопросы

1.  с чем связан переходной процесс в электрической цепи.

       1. изменением энергетического состояния энергоемких элементов.

       2. С характером входных сигналов.

       3. С мгновенным изменением напряжения и тока на энергоемких элементах.

       4. С мгновенным изменением напряжения и тока на резистивных элементах.

3. Что такое переходная характеристика электрической цепи.

1.  Отклик на единичное  ступенчатое воздействие.

2.  Отклик на произвольное воздействие.

3.  Зависимость коэффициента передачи цепи от частоты.

4.  Зависимость коэффициента передачи цепи от времени.

4. Каков характер переходной характеристики в цепи первого порядка.

      Апериодический. 2. Колебательный. 3. Критический. 4. Апериодический и колебательный.

5.  На вход цепи с операторной передаточной функцией вида К_u(p)=(1+pτ)^-1 воздействует гармонический сигнал s₁(t)=Acos(ωt). Записать отклик.

1. s₂(t)=[(1+(ωτ)²)^0.5]cos(ωt).   2. s₂(t)=[(1+(ωτ)²)^0.5]cos(ωt- ωτ).

3. s₂(t)=[(1+(ωτ)²)^0.5]cos(ωt+ ωτ).    4. s₂(t)=[(1+(ωτ))]cos(ωt).

6.  Нарисовать схему замещения при ω→0.

1.                              2.                          3.                          4.

7. 

На вход цепи (рис.3) воздействует ступенчатое напряжение. Рассчитать вы ходное напряжение при t→∞.

1. 0.     2.  E R2/(R1+R2).    3. E R1/(R1+R2).   4. E.

8.  Нарисовать схему замещения цепи (рис.6а) при ω→0.

1.  2.  3.  4.

9. 

Нарисовать схему замещения при ω→∞.

1.  2.  3.  4.

10.  На вход цепи (рис.13) воздействует ступенчатое напряжение. Рассчитать выходное напряжение при t→0.

1. 0.     2. E R2/(R1+R2).    3. E R1/(R1+R2).   4. E

11.  Первый закон коммутации в электрической цепи с индуктивностью записываются в следующем виде

1) i_L(0+)= i_L(0-);          2) u_L(0+)= u_L(0-);   3) i_l(0+)= i_L(0-)=i_{L уст}

12.   Переходный процесс установления тока в электрической цепи первого порядка описывается выражением

       1) i=A₁e ^{P1 t} + A₂e ^{P2 t} ;                2) i=i_уст.+ Ae ^{P t +};               3) i= A₁e ^{P1 t}

13.  Постоянная времени интегрирующей RC-цепи определяется выражением

1.t=R/C.              2) t=(RC)^-1. 3) t=RC.

14.  Как формулируется один из важнейших законов ОТЦ – закон коммутации?

а) Напряжение на емкости или ток через индуктивность не могут измениться скачкообразно;

б) Перемена активных сопротивлений местами в цепи не меняет характеристики цепи;

в) Токи в узле не могут только сходиться или только вытекать из узла;

г) При скачкообразной подаче тока или напряжения через индуктивность или емкость выходной ток или напряжение устанавливаются моментально;

15.  На каком виде преобразования основан операторный (операционный) метод анализа электрических цепей?

а) Преобразование Фурье;   б) Преобразование методом интеграла Дюамеля;

в) Эквивалентное преобразование электрической цепи;   г) Преобразование Лапласа;