Используя, определение KU(jw) получим его выражение Ku(jw)=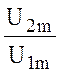 =
=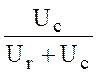 =
=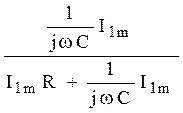 =
=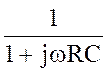 .
.
Определим АЧХ и ФЧХ для Ku (jw) и построим их графики (рис.5.11.), подсчитав значения при w=0, w=¥.
Вспомним,
что z=![]() =
=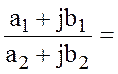
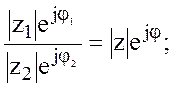 где:
где: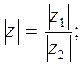
![]() тогда,
тогда,
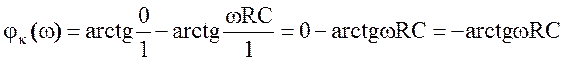 |
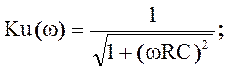 Ku(0)=1; Ku(¥)=0.
Ku(0)=1; Ku(¥)=0.
Отсюда следует: φк(¥)= π/2, φк(0)= 0.
Такая цепь пропускает сигналы низких частот (Ku(0)=1) и подавляет сигналы высоких частот (Ku(¥)=0) и называется фильтром низких частот (ФНЧ).
Граничная частота определяется
из выражения 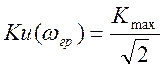 . Рассчитаем ее для нашего
примера:
. Рассчитаем ее для нашего
примера:
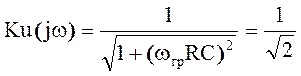 , wгрRC=1 Þ
, wгрRC=1 Þ 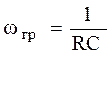 . Построить годограф частотно-передаточной
функции (годограф иногда называют АФЧХ).
. Построить годограф частотно-передаточной
функции (годограф иногда называют АФЧХ).
При ![]()
![]()
![]() .
.
При ![]()
![]()
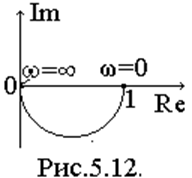
Учитывая, что реальная часть всегда положительна и уменьшается от 1 до 0, а мнимая часть всегда отрицательна, можно построить график годографа (рис. 5.12.).
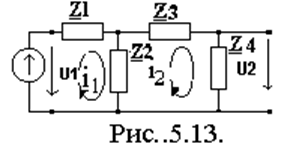
 Пример 3. Для обобщенной двухконтурной цепи, представленной
комплексной схемой замещения (рис.5.13), рассчитать ее частотные
характеристики:
Пример 3. Для обобщенной двухконтурной цепи, представленной
комплексной схемой замещения (рис.5.13), рассчитать ее частотные
характеристики:
1. Zвх(jw), Zвх(w), jz(w). 2.K(jw), K(w), jk(w).
Решение. 1) Найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления.
 |
2. найдем КЧХ коэффициента передачи по напряжению. По определения Ku(jw)=Ů2m/Ů1m , а Ů2m=Z4İ2 – находим по закону Ома.
Отсюда видно, что для расчета КЧХ необходимо найти İ2. Находим İ2 методом контурных токов. Для этого: определим число независимых контуров: Nk=в-у+1=3-2+1=2, каждому из них присвоим свой контурный ток İ1, İ2 и составим уравнения по методу контурных токов.
![]() Z11İ1+Z12İ2=E11
Z11İ1+Z12İ2=E11
Z21İ1+Z22İ2=E22 ,
где: Z11 – собственное сопротивление первого контура, Z11=Z1+Z2;
Z12 и Z21 сопротивление смежных контуров, Z12= Z21= - Z2 ;
Z22-собственное сопротивление II контура. Z22=Z2+Z3+Z4 ;
Ė11-алгебраическая сумма источников ЭДС I-ого контура, Ė11=U1m;
E22- алгебраическая сумма источников ЭДС II-ого контура, во II контуре источников ЭДС нет, Ė22=0.
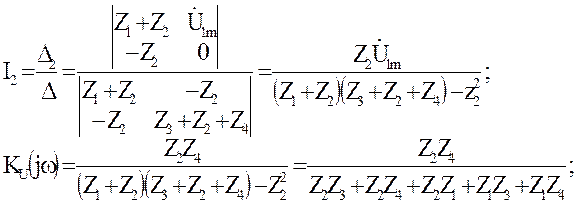 |
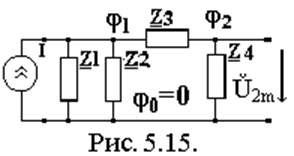
Покажем другой способ нахождения КЧХ коэффициента передачи по напряжению. Найдем КЧХ, используя для расчета U2m метод узловых потенциалов. Для этого:
· преобразуем исходную схему к виду, показанному на рис.5.15, заменив источник эдс на источник тока;
· потенциал узла 0 примем равным нулю, j0=0;
· тогда Ů2m=j2 - j0= j2.
Составив уравнения по методу узловых потенциалов, получим систему второго порядка и решим ее, относительно j2, по методу Крамера:
![]() Y11j1+ Y12j2=I11
Y11j1+ Y12j2=I11
Y21j1+ Y22j2=I22,
где: Y11 – собственная проводимость первого узла, Y11=(1/Z1)+(1/Z2)+(1/Z3);
Y12 и Y12 – межузловая проводимость Y12= Y21= - 1/Z3; =-1/Z3;
Y22 - собственная проводимость первого узла Y22=(1/Z3) +(1/Z4);
j1, j2 – потенциалы первого и второго узлов;
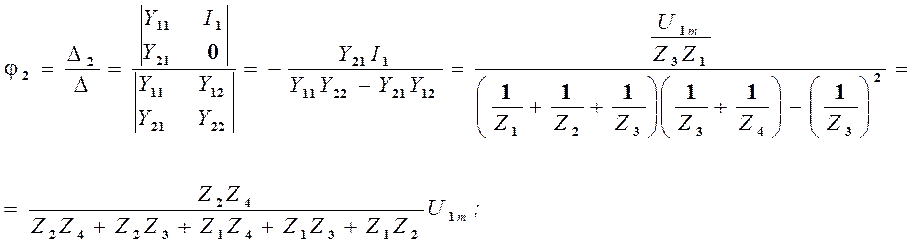 |
Ku(jw)=Ů2m/Ů1m =Z2Z4/(Z2Z4+Z2Z3+Z1Z2+Z1Z3+Z1Z4).
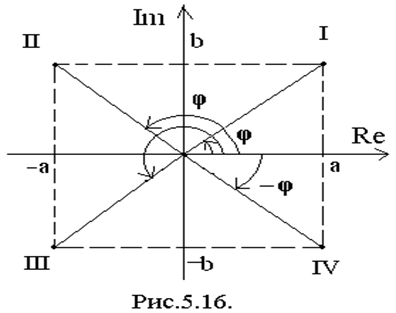
Для построения ФЧХ необходимо пользоваться следующими формулами.
![]() , где a -
реальная часть, а b - мнимая.
, где a -
реальная часть, а b - мнимая.
ΦZ = ![]()
I ![]() a
> 0, b>0; φ = arctg
a
> 0, b>0; φ = arctg![]()
II ![]() a<0, b>0; φ =
a<0, b>0; φ = ![]() - arctg
- arctg![]()
III ![]() a<0, b<0; φ =
a<0, b<0; φ = ![]() + arctg
+ arctg![]()
IV ![]() a>0,
b<0; φ = - arctg
a>0,
b<0; φ = - arctg![]()
5.5. Резонансные цепи. Колебательные контуры
Явление резкого возрастания амплитуды отклика при приближение частоты внешнего воздействия к определенному значению частоты называется резонансом. Такой резонанс имеет место в механике и называется амплитудным резонансом. Частота, на которой выполняется условие резонанса, называется резонансной частотой
В электротехнике, величины характеризующие режим работы цепи на разных элементах имеют амплитудный резонанс на разных, хотя и близких частотах. Поэтому в теории цепей под резонансом понимаю фазовый резонанс. Под фазовом резонансом понимают условие, при котором цепь, содержащая реактивные (L и C) элементы, имеет входное сопротивление резистивное, т.е. при резонансе ток и напряжение находятся в одной фазе, как и на любом резистивном элементе, а сдвиг по фазе равен нулю.
Электрические цепи, в которых имеет место явления резонанса, называются резонансными. Поскольку переходные характеристики резонансных цепей имеют колебательный характер, то резонансные цепи называют колебательными контурами.
Колебательные контура используются для решения задач частотной избирательности. Под частотной избирательностью понимают способность цепи выделять сигналы узкого диапазона частот. К простейшим колебательным контурам относят последовательный и параллельный колебательный контур, также систему связанных контуров.
5.5.1. Последовательный колебательный контур
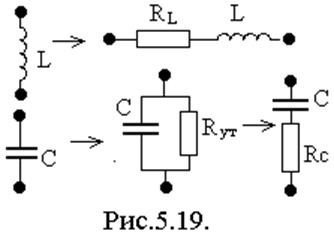
Последовательный колебательный контур состоит из последовательного соединения индуктивности L и емкости C (рис.5.17).
 |
Определим частотную характеристику входного сопротивления последовательного колебательного контура.
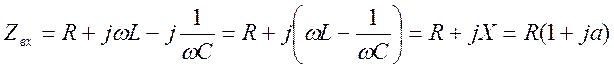 ;
;
где R и 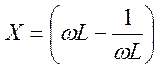 – резистивная и
реактивная составляющая сопротивления последовательного колебательного контура;
– резистивная и
реактивная составляющая сопротивления последовательного колебательного контура;
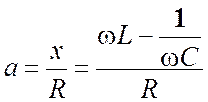
![]() - обобщенная расстройка
колебательного контура.
- обобщенная расстройка
колебательного контура.
Характер входного сопротивления Zвх(jω) зависит от частоты.
1)
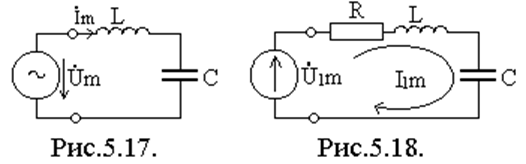
На низких частотах (НЧ) 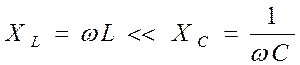 ; X < 0.
Это означает, что сопротивление носит емкостной характер, его можно
представлять эквивалентной схемой приведенной на рис.5.20.
; X < 0.
Это означает, что сопротивление носит емкостной характер, его можно
представлять эквивалентной схемой приведенной на рис.5.20.
2) На высоких частотах (ВЧ) 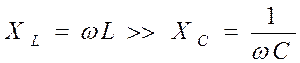 ,
Х > 0, сопротивление последовательного контура носит индуктивный
характер (рис.5.20б).
,
Х > 0, сопротивление последовательного контура носит индуктивный
характер (рис.5.20б).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.