Электротехника \ Электроника

Частотные характеристики и операторные функции электрических цепей, страница 3

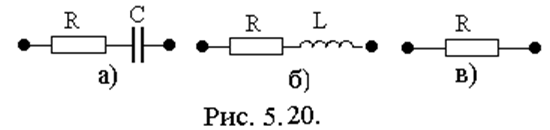
3) На некоторой частоте , , 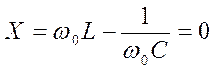Х=0, сопротивление контура имеет резистивный характер, а его схема замещения  состоять из резистора R.

Частота, на которой выполняется это условие, называется резонансной, она определятся как ω0=(LC)-1/2 .

Отметим свойства последовательного контура на резонансной частоте:

1)  сопротивление имеет резистивный характер и минимально по сравнению с сопротивлением на других частотах.

2) Начальные фазы напряжения и тока на контуре одинаковы φu=φi, сдвиг по фазе равен   φ=φu-φi=0.

3) Амплитуда тока в контуре максимальна и равна  .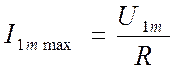

4) Сопротивления реактивных элементов L и C одинаковы и равны - характеристическому сопротивлению контура т. е. .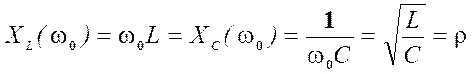

5) Амплитуда напряжений на реактивных элементах контура одинаковы и в Q – добротность раз больше (амплитуды напряжения на входе).

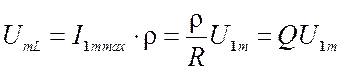, Q- добротность контура, .

Поэтому  резонанс в последовательном контуре называется резонансом напряжений.

6) Амплитуды напряжений на реактивных элементах находятся в противофазах, а поэтому суммарное напряжение на реактивных элементах равно нулю:  .

Построим графики АЧХ и ФЧХ входного сопротивления последовательного контура (рис. 5.21). Для построения учтем, что

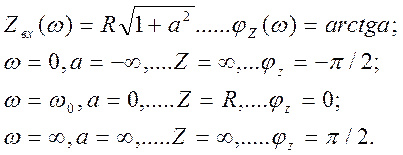
5.5.1.1. Резонансная характеристика последовательного колебательного контура - это есть зависимость от частоты отношения комплексной амплитуде тока к комплексной амплилитуде тока при резонансной частоте, т.е. -.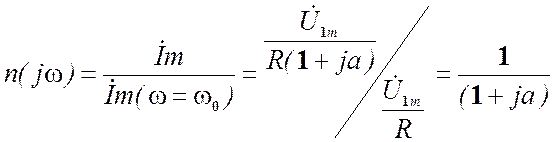

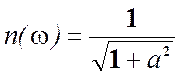Отсюда АЧХ:   ; и ФЧХ:   .

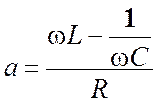 – обобщенная расстройка

         

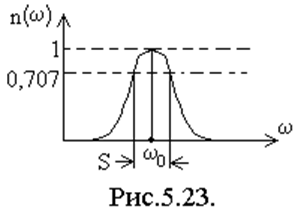
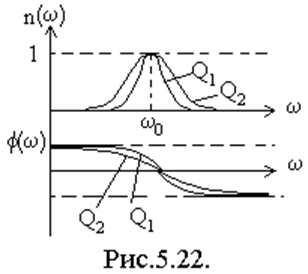
 На остальных частотах резонансная характеристика убывает.

Важным параметром колебательного контура является его полоса пропускания (S). Это диапазон частот, в котором резонансная характеристика превышает уровень 1/√2 т.е. 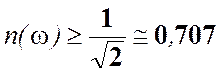. S=ωв - ωн, где ωв, ωн верхняя и нижняя граничные частоты полосы пропускания.

Параметры контура S, Q и ω0 связаны соотношением 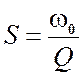. Отсюда следует, чем больше добротность, тем меньше полоса пропускания, тем лучше избирательные свойства колебательного контура.

5.5.1.2. Зависимость добротности контура Q от сопротивления источника сигнала (Ri) и сопротивления нагрузки (Rн)

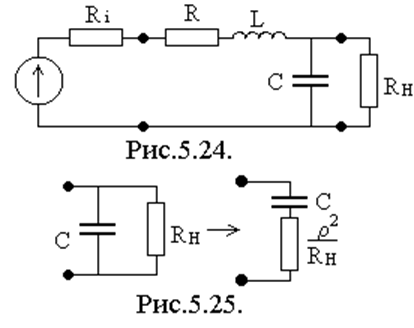Схема замещения последовательного колебательного контура с учетом добавочных элементов Ri, RH имеет вид (рис.5.24).

На рис. 5.25 показано эквивалентное преобразование паралельной RC цепи в последовательную, где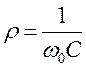. Добротность контура с учетом добавочных элементов Ri, RH называется эквивалентной и определяется из следующего выражения

 .

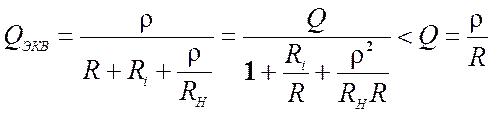Она меньше собственной добротности контура Q. Для того, чтобы  необходимо:

1) . Это означает, что последовательный колебательный контур необходимо питать от источника ЭДС, т.е. источника с нулевым сопротивлением.

2) . В этом случае нагрузка не будет влиять на добротность контура.

5.5.1.3. Последовательный колебательный контур как четырехполюсник

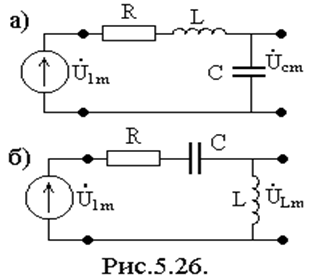На практике используются две  схемы включения рис.5.26. Для четырехполюсника основной частотной характеристикой является передаточная по напряжению.

1)

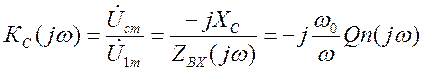
2)

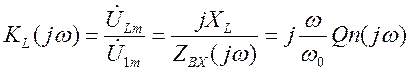
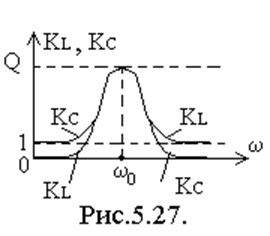
Построим графики амплитудно-частотные характеристик этих зависимостей рис.5.27. Подробный анализ показывает, что при высоких добротностях резонансные частоты обеих схем совпадают и равны ω0.

5.5.2. Параллельный колебательный контур

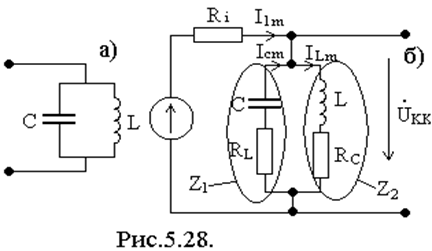
Он состоит из параллельно соединенных двух реактивных элементов L и C. Его принципиальная схема имеет вид, приведенный на рис.5.28а.

Схема замещения контура с учетом резистивных  потерь реактивных элементов приведена на рис.5.28б.

Определим комплексное входное сопротивление параллельного колебательного контура

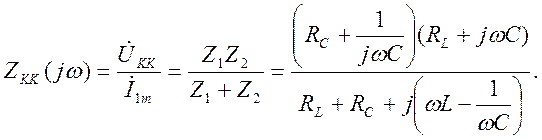
Обозначим - общие резистивные потери параллельного контура. При условии, что вблизи от резонанса, 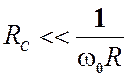. Получим окончательное выражение для  сопротивления параллельного колебательного контура.

.

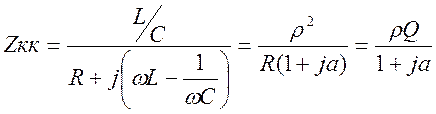Характер сопротивления параллельного колебательного контура зависит от частоты.

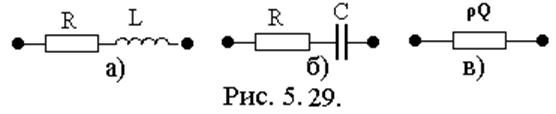
1) На НЧ 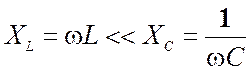- характер индуктивный. Схема замещения состоит из элементов R, L и приведена на рис. 5.29а. Сопротивление контура Zkk(ω = 0) =RL.

2) На ВЧ  - сопротивление носит емкостной характер, рис. 5.29б. Сопротивление контура Zkk(ω ®µ) =RC.

3) На , когда  сопротивление контура имеет резистивный характер Zkk(ω0) =ρQ, рис. 5.29в, где ω0=(LC)1/2 – резонансная частота.

Отметим свойства параллельного контура на резонансной частоте.

1)  Сопротивление контура имеет резистивный характер и его модуль имеет максимальное значение по сравнению с сопротивлением на других частотах.

2)  Ток и напряжение совпадают по фазе.

3)   сопротивление реактивных элементов одинаково и равно .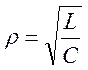

4)  Амплитуда тока через реактивные элементы в Q раз превышает ток во внешней цепи: 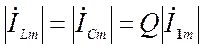, поэтому резонанс в параллельном контуре называется резонансом токов.  Это вытекает из следующего

; .

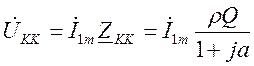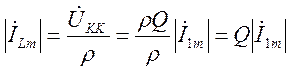5)  Токи через реактивные элементы сдвинуты по фазе на 1800.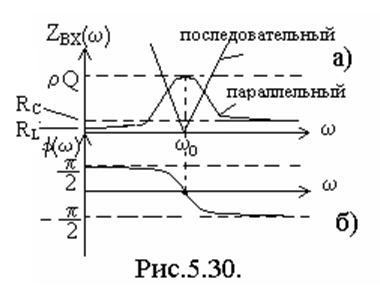

Построим графики АЧХ  и ФЧХ входного сопротивления параллельного контура, которые определяются выражениями

АЧХ: 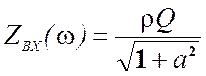; ФЧХ: .

Построенные графики приведены на рис.5.30.

5.5.2.1. Резонансная характеристика параллельного колебательного контура

Она представляет собой зависимость от частоты отношения комплексной амплитуды напряжения на контуре к амплитуде напряжения на резонансной частоте.

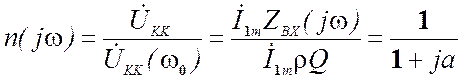
Вид резонансной характеристики для последовательного и параллельного контуров одинаковы, это их и объединяет. По характеру зависимости сопротивления от частоты они обладают противоположными свойствами (см. рис.5.30).

5.5.2.2. Влияние сопротивлений источника сигнала и нагрузки на добротность параллельного колебательного контура

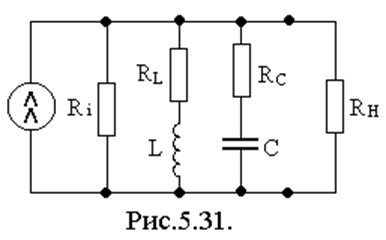Схема замещения контура с учетом этих добавочных элементов приведена на рис.5.31.

Добротность контура с учетом паразитных элементов называется эквивалентно и подсчитывается из выражения

.

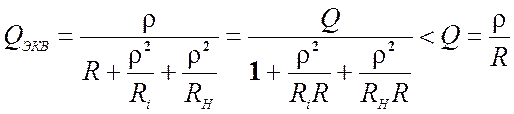Для того, чтобы , необходимо:

1) , т.е. контур питать от источника тока.

2) , т.е. контур по выходу должен работать в режиме холостого хода.

5.6. Связанные колебательные контуры

Совокупность двух или более колебательных контуров, между которыми существует электрическая и магнитная связь, а энергия из одного контура может 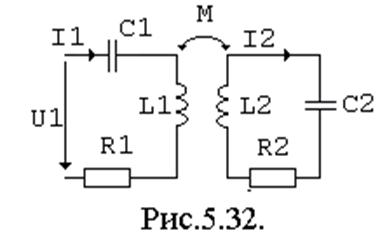передаваться в другой, называется связанными колебательными контурами. Рассмотрим в качестве примера двухконтурную схему с трансформаторной связью.

Скачать файл