2) Коэффициент динамичности – Kд, характеризует максимальные отклонением выходного сигнала от его значения в установившемся конечном состоянии.
3) Колебательность – K, определяет число колебаний за время tП.
Длительность перех. процесса, даже при быстром затухании динамич процесса теоретически бесконечна, поэтому на практике считают переходный процесс завершенным, если значение выходного сигнала перестает отличаться от установившегося конечного значения не более чем на опред. величину - коридор стабилизации установившегося состояния Δ = 5%·|v(t)-v(∞)|
Время перех. процесса - интервал времени от момента начала ступени сигнала воздействия до последнего пересечения переходной характерной линии коридора стабилизации. Это характеризует быстродействие тех. системы.
Коэффициент динамичности определяется по формуле: Кд = 1+Amax/ ΔV где
Amax – max амплитуда отклонения выходного сигнала V от конечного установившегося ее значения. Amax =max|UЭi-U∞| где Vэi – i-e экстремальное значение фазовой координаты определяемое из условия dv/dt=0
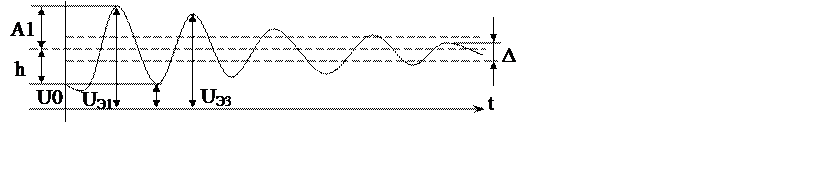 |
Декремент колебаний определяется по формуле D=A1/A2, где А1,А2 – амплитуды 2-х смежных отклонений фазовой координаты от значения V∞. Чем выше значение D, тем быстрее затухают колебания.
Колебательность К определяется числом амплитудных значений VЭi за время tП или числом полупериодов колебаний. При высоких требованиях к переходным процессам K<2, при умеренных K<5.
27. Задачи идентификации в моделировании. Условия идентификации
Задача идентификации: по заданному входному воздействию и выходному сигналу найти оператор системы: вход-(?)оператор-выход
Идентификация - построение модели объекта или системы на основе экспериментального исследования. Для физич объекта м.б. построено много разных, но эквивалентных моделей. Задача идентификации состоит в отыскании оптимальной в соответствии с выбранным критерием модели.
Модель линейной системы имеет вид dx/dt=Ax. Пусть выполнены исследования по модели в момент времени t=kτ, k=0,1…m;
В соответствии с формулой Коши: x(τ)=eAτx(0)
x(2τ)=eAτx(τ)
…
x(mτ)=eAτx((m-1)τ)
Это отношение можно переписать в виде
[x(τ)x(2τ)…x(mτ)]=eAτ[x(0)x(t)…x((m-1)τ)]
Обозначим через L(τ) и k(τ) матрицы левой и правой частей L(τ)= eAτk(τ)
eAτ=L(τ)k-1(τ) Значит матрица eAτ может быть найдена по (m+1) изменению вектора x. Это св-во модели - идентифицируемость.
28. Параметрическая идентификация
Задача идентификации: по заданному входному воздействию и выходному сигналу найти оператор системы: вход-(?)оператор-выход. Цель идентификации объекта — определение вида оператора связывающего входной сигнал x(t) с выходным сигналом на интервале времени. Следует подобрать такой оператор модели, при котором ее выходные сигналы были максимально приближены к сигналам на выходе реального объекта или системы.
При экспериментальном подходе осуществляют подбор адекватной структуры модели и выбор входного воздействия x(t) так, чтобы по результатам эксперимента можно было найти оценки всех параметров модели. Отсюда, идентификацией динамического объекта - процедура определения структуры и параметров его модели, которые при одинаковых входных сигналах для модели и объекта обеспечивают близость выхода модели к выходу объекта при наличии определенного критерия качества. При этом критериями близости выходных сигналов модели и объекта могут быть: среднеквадратичная, абсолютная, относительная погрешности, максимум правдоподобия и др. Параметрическая идентификация модели по этим критериям осуществляется с помощью методов поиска экстремума, основными из которых являются: метод Ньютона-Канторовича; градиентный метод; метод случайного поиска и др. Часто исп рекуррентный метод наименьших квадратов. Определение параметров можно свести к задаче параметрической оптимизации – минимизации ошибки моделирования.
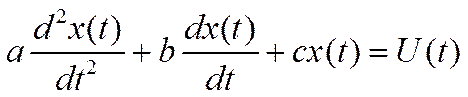 Пример:
Динамика технического объекта описывается дифуром 2-го порядка.
Пример:
Динамика технического объекта описывается дифуром 2-го порядка.
Пусть по данным эксперимента известны функции u1(t) – внешнего воздействия и x1(t) – выходного сигнала на интервале времени [0,τ].
Ошибка моделирования определяется как функция параметров a,b,c.
Здесь x(t,a,b,c) – решение дифура.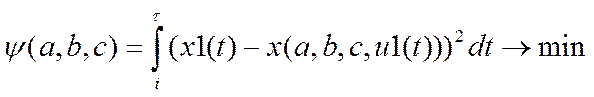
Для реализации численных методов
вводится дискретное время:
tK=kΔt k=0,1,…,n; n= τ/Δt Тогда диф. оператор можно заменить конечными разностями, интегральный – кон. суммами и min полученную Σ по параметрам.
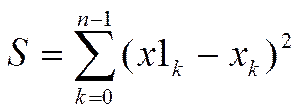 |
29. Идентификация во временной области
Если из результатов эксперимента известно 2 ф-ции u(t) и x(t), то в задачу идентификации входит восстановление диф или интегр оператора связи между этими функцими.
30. Способы создания графического пользовательского интерфейса в Matlab.
В основе подхода к созд. графич. пользоват. интерфейса в MatLab лежат принципы объектно-ориентированного программирования.
![]() Root
Root
![]() Figure
Figure
![]()
![]()
![]()
![]()
image line … text
Корнем дерева явл. класс Root, символизирующий экран дисплея. Графич. окно явл. объектом класса Figure. Объект Axes, представляющий график функции в графич. окне, явл. сложным и многокомпонентным объектом.
Все объекты создаются функциями конструкторами, имеющими имена, совпадающие с названием этих объектов. Конструктор можно вызвать как с параметрами, так и без них.
Для идентификации различных объектов существует термин handle – указатель, дескриптор. В каждый конкретный момент выполнения программы выделяют три объекта:
1) активное окно (current figure)
2) активный графич. объект (current object)
3) активный график (current axes).
Для получения значений дескрипторов этих объектов используют три сист. фун.:
1) gcf – get current figure 2) gco - get current object 3) gca - get current axes.
Полученными значениями можно манипулировать при работе программы.
Есть два способа организации GUI: 1) непосредственный 2) автоматизированный
Непосредственный – GUI программируется функциями непосредственно в М-файле.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.