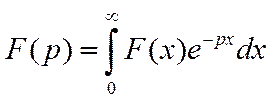Другие предметы \ Моделирование систем управления

Роль моделирования в технике. Основные определения теории моделирования. Описание процесса компьютерного моделирования. Технические объекты моделирования, параметры объектов. Классификация моделей. Требования к моделям. Обзор методов построения математических моделей, страница 6

Рассмотрим функцию вещественных переменных х, на которую наложены ограничения: при x<0 F(x)=0; Преобразование Лапласа от функции F(x) - функция от комплексной переменной p=s+iσ Сама функция - оригинал, а F(p) – её изображение.                                    Не только f(x) однозначно определяет F(p), но и

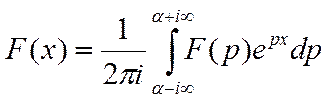 наоборот, F(p) однозначно определяет f(x). Это соответствие дается формулой обращения или формулой Меллика.

Т.о., существует взаимно однозначное соответствие  F(x) ó F(p). Свойства:

Дифференцирование оригинала – операция дифференцирования оригинала заменяется операцией умножения изображения на p.

 


Оригинал

A

 eαt

sin(wt)

Хэвисайд H(t)

Дельта фун. Δ(е)

Изображение

A/p

1/(p-1)

w(p2+w2)

1/p

1

Интегрирование оригинала – операция интегрирования оригинала заменяется операцией деления изображения на p

 


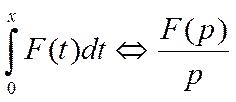23. Передаточная функция, ее получение для динамических моделей

Передаточная ф-ия– один из способов мат описания динамич системы. Она представл диф. оператор, выражающий связь между входом и выходом системы. Зная вх сигнал системы и передаточную ф-ию, можно восстановить вых сигнал.

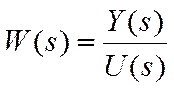Пусть U(t) – входной сигнал, а y(t) – её выходной сигнал. Тогда передаточная функция W(s) такой системы записывается в виде:

Где U(s) и Y(s) – преобразования Лапласа для сигналов u(t) и y(t) соответственно.

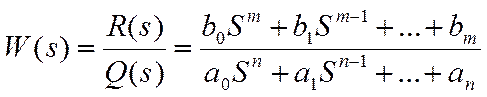Передаточная функция – это дробно-рациональная функция комплексной переменной (s):

Знаменатель передаточной функции – это характеристический полином системы.

Полюсы передаточной ф-ии – это корни соотв характеристического полинома.

Амплитудно-фазовая частотная характеристика системы можно получить из передаточной ф-ии с пом формальной замены комплексной переменной s на jw.

W(jw)W(s), s=jw;

Получить передаточную функцию для механической системы по виду дифура.

 


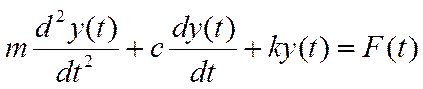Выполним преобразование Лапласа

m·S2·Y(s)+c·s·Y(s)+k·Y(s)=Z(s)         Находим передаточную функцию

  

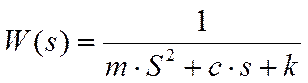
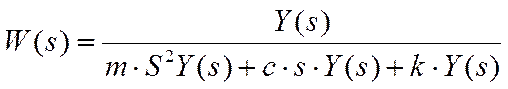
24. Алгоритм реализ динамич моделей с исп передаточной функции  в СКМ.

1)  Определить функцию входного воздействия F(t)

2)  Выполнить преобразование Лапласа над функцией F(t)

3)  Задать передаточную функцию W.

4)  Получить операторное изображение выходной функции системы, умножив операторное изображение входной функции на передаточную функцию.

5) 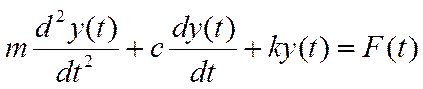 Выполнить над выходной функцией обратное преобразование Лапласа и получить функцию выходного сигнала в временной области.

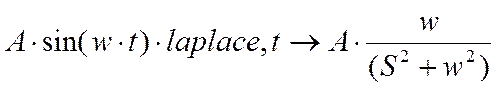Задаем входной сигнал A·sin(w·t), выполняем  преобразование Лапласа

 


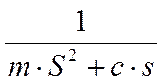Задаем передаточную функцию в общем виде

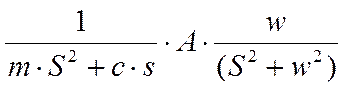Выполняем умножение операторных изображений вх сигнала и передаточной функции, получаем изображение вых сигнала

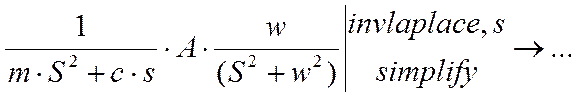Выполняем обратное преобразование Лапласа, получаем функцию выходного сигнала в общем виде

Задаем конкретные исходные данные, например A:=1.9  w:=5  m:=10  c:=2  H:=10

Создаем функцию выходного сигнала и табулируем ее.

F(t):=полученному от преобразования Лапласа и упрощения

t:=0,0.01..50 и строим график

Рассмотрим вычисление амплитудно-фазо-частотной хар-ки. Рассмотрим сначала АЧХ. Строим АЧХ, подставив в передаточную функцию jw

 


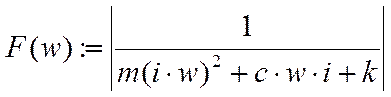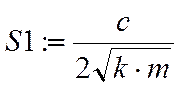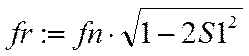– разрешающая частота.

 


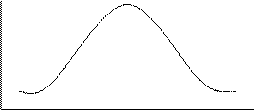Табулируем w1:=0,0.0001..2  и строим F(w1)

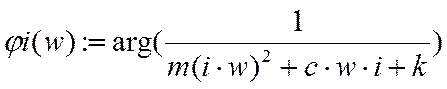Строим АФЧХ


25. Исследование динамических моделей в СКМ.

Для динамических систем ставятся 4 группы задач:

–  Задачи анализа

–  Задачи синтеза

–  Идентификации

–  Обратные задачи

Для линейных динамических систем ставятся следующие задачи анализа:

–  Анализ выходных процессов

–  Анализ устойчивости

–  Анализ чувствительности

–  Анализ управляемости

Для динамич моделей можно проводить след виды анализа выходного сигнала:

–  Влияние изменения начальных условий на выходной сигнал

–  Влияние изменения внутренних параметров на выходной сигнал

–  Влияние изменения пар-ов возмущающих воздействий на выходной сигнал.

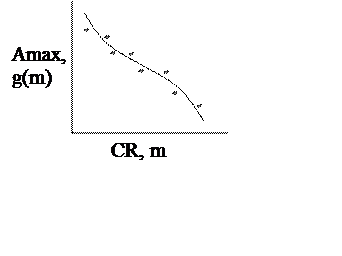
Пример для 2.

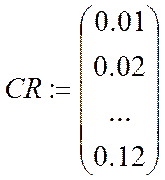– вектор значений изменяемого внутреннего параметра

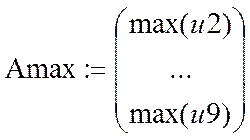– экстремальное значение выходного сигнала.

Выполняем аппроксимацию

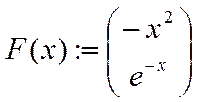     H:=linfit(CR,Amax,F)    g(m):=F(m)·k     m:=0,0.01..0.13

      

Задачи синтеза: по желаемому выходу найти входной сигнал и оператор системы (неопределённые параметры оператора)

Задачи идентификации: по заданному входному воздействию и выходному сигналу определить оператор системы.

Информация, полученная экспериментальным путём о входном и выходном сигнале, использованная для определения неизвестных параметров системы при известной структуре модели. (Модель в виде «серого» ящика).

Обратная задача получает сигнал при заданном вых сигнале и операторе системы.


26. Исследование переходных процессов в Mathcad

Любое изменение внешних управляющих сил возмущающих воздействий приводит к возникновению переходного процесса. При изменении внешнего воздействия u(t) любой выходной сигнал технической системы v(t) может быть представлен состоящим из 2-х составляющих:  V(t)=VB(t)+VП(t), где

VB(t) – вынужденная составляющая, определяемая частным решением неоднородного ДУ, описывающего функционирование динамич тех системы.

-VП(t) – переходная составляющая, характеризующая свободный переходный процесс и определяемая общим решением однородного ДУ без правой части.

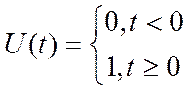Если тех. система устойчива, переходная составляющая с течением времени затухает и остается лишь вынужденная составляющая. Качество переходных процессов важно для устойчивых систем. Переходная хар-ка - реакция тех. системы на ступенчатое воздействие, ее рекомендуют получать при нулевых начальных условиях и единичном ступенчатом воздействии.

Для оценки качества переходного процесса используют следующие показатели:

1)  Время переходного процесса – tП, характеризуется длительностью пребывания технической системы в неустановившемся состоянии.

Скачать файл