Роль моделирования в технике. Основные определения теории моделирования. Описание процесса компьютерного моделирования. Технические объекты моделирования, параметры объектов. Классификация моделей. Требования к моделям. Обзор методов построения математических моделей, страница 13

Линейные стационарные системы в Simulink моделируются как блочные схемы с участием блока Transfer Fcn , который задает звено модели через передаточную функцию. Обратную связь моделируется блоком сумматор.

Ступенчатое воздействие задается блоком Step

 

LTI-Viewer - обозреватель lti-объектов служит для исследования процессов ЛСС в интерактивном графическом режиме. Он позвол строить графики временных и частотных характеристик нескольких объектов в одном графич окне и олучать числовые параметры моделей. Вызов LTI-Viewer команда ltiView. НАчало работы с обозревателем:

- загрузка lti-объекта - File-Import.

- определить кол-во и виды графиков, выводимых в окно обозревателя Edit-Plot Configuration

- настроить параметры графиков Edit-View Preferences

В качестве параметров могут выступать:

Units - ед. измерения - радианы/сек, децбелы, герцы (для частотных), абсолютные единицы (для АЧХ), градусы, радианы (для фазы).

-style - установка координатной сетки, разметка осей графиков

- parameters - установка значения диапазона времени и частоты для простроения графиков и диаграмм.

Задача синтеза регуляторов в динамич системе включ выбор структуры и параметров регулятора при известных параметрах объекта управления и заданных динамических характеристиках исслед системы. Критерии: временные и частотные критерии качества.

Один из параметров переходного процесса - максимальное перерегулирование в процентах по выражению: σ =(Ymax-Yуст)/Yуст*100%

Проектирование регуляторов включает задачи:

- выбор места включения регултора

- выбор типа и расчет пар-ов регулятора, придающего системе заданные мех св-ва

Регулятор м.б. непрерывным и цифровым. Для синтеза регуляторов есть средство rltool.

1. Запускаем >>rltool

2. Выбор передаточной функци для модели импортированием

3. Получение графич хар-к модели корневой годограф сразу после ввода исх данных. Можно получить графки перех процесса, диаграммы Боде, Найквиста

4. Получение схемы Simulink: Tools-Draw Simulink

48. Оптимизация параметров САУ.

В MatLAB включен пакет, позволяющий оптимизировать параметры переходного процесса модели ЛСС, изменяя параметры регулятора самого объекта управления.

Этот пакет называется Simulink Response Optimization. Рассмотрим блок Signal Constraint. Последовательность работы с блоком:

1. Создаётся модель исследуемой динамической модели в Simulink

2. Вход блока Signal Constraint соединяется с тем сигналом, на который накладывается ограничение.

3. Задаются начальные параметры, подлежащие оптимизации.

4. Открывается окно блока Signal Constraint

5. Задаются параметры переходного процесса:

- с помощью перемещения линий ограничения

- с помощью команды Goals- Respons

6. Задаются параметры, подлежащие оптимизации с помощью команды меню Optimization – Tuned Parameters

7. Инициализируется процесс оптимизации модели нажатием кнопки Start.

Для переходного процесса задаются следующие параметры:

- длительность – Setting time

- время нарастания – Rise time

- макс перерегулирование – Overshoot

- макс недорегулирование – Undershoot

49. Опред. событийно-упр систем. Понятия теории конечных автоматов

СУС - системы, при моделир которых исп: - непрерывные модели (системы ДУ) и дискретные модели (конечные автоматы). Эти 2 вида моделей опираются на разные модели времени – дискретные или мгновенные для дискр моделей, и непрерывные или длительные для непрерывных. Такие системы - гибридные или непрерывно-дискретные. Какая бы модель времени не исп, поведение гибридной сист с вых пар-ми y(t) в любой момент времени t* характ парой (t*, y(t*)) - событием. У него 2 коорд: временная t* - указывает на время наступления события и пространственная y(t*) – характ явление (указывает на процесс). Если простр-временные координаты непрерывны, то пара (t,y(t)) определяет бесконеч множество событий. Если пара y(t) дискретна, то события - дискретные и изображаются в виде графа. Пример: описать функционирование светофора с помощью переходной функции:   Свет (i+T) = свет(i), T=3, i=1,2,3…  

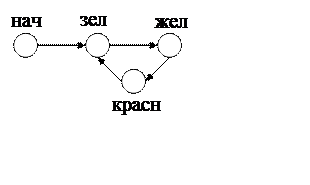Свет: зелёный (i=1), жёлт (i=2), красный (i=3)

Параметры гибридных систем: - системы управления техпроцессами, - сложные бытовые приборы, - военная область, - космонавтика, транспорт и связь. Все эти системы сост из аналоговых и дискретных элементов.

Ограничение числа пар-ров АА определило понятие конченый автомат (КА) – абстракция позволяющая описать пути изменения сост

Автомат можно представить как нек уст-во, на кот подаются вх сигналы и снимаются вых, кот могут иметь нек внутренние сост. При анализе автоматов, изучают их поведение при разных возмущающих воздействиях, и min число состояний автомата без работы по заданному алгоритму. Такой автомат – абстрактный (АА) – мат. абстракция, модель дискретного уст-ва, имеющая 1 вход, 1 выход, и в каждый момент времени находящаяся в 1 состоянии из множества возможных. На вход уст-ву символы одного языка, на выходе он выдаёт символы (в общем случае) другого языка. Формально, АА определяется как пятёрка H=(S,X,Y, δ, λ), где S – конечное множество состояний автомата, X,Y – конечный вх и вых алфавиты, из которых формир строки, считываемые и выдаваемые автоматом.    δ: S*X → S – функция переходов,  λ: S*X → Y – функция выходов. Функциональная схема абстрактного автомата:

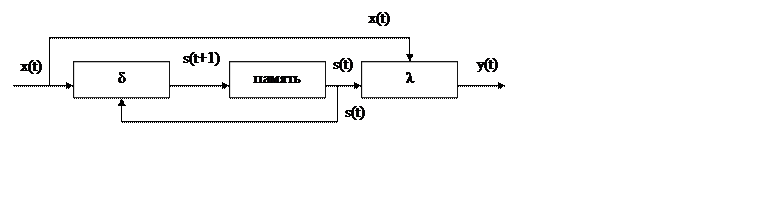
объекта в завис от его тек сост и вх данных, при условии, что общее возможное кол-во состояний конечно. По способу формир функций выхода: автоматы Мили и Мура. В авт Мили функцию выходов λ опред значение вых символа по классич схеме АА. Особенность авт Мили, что функция выходов - двухаргументная и символ в выходном канале y(t) обнаруживаются только при входном канале x(t). Зависимость вых сигнала только от состояния представлен в автомате Мура, здесь функция выходов опред значение вых символа только по 1 аргументу - состоянию автомата. Рисунок такой же (без верхней передачи x(t) и вместо λ надо μ.

50. Пакет Stateflow: общий обзор