Интерполяция - замена исходной F(X) функцией φ(x), так чтобы φ(x) точно проходила ч/з точки исх функции. Интерполяция частный случай аппроксимации (точечная). Точки исх функции – узлы интерполяции. Экстрополяция - аппроксимация вне заданной области определения исх функции.
Мера отклонения функ F(x) от φ(x) - величина, равная сумме квадратов разностей между аппроксимирующей и исх функ и она должна стремиться к min.
Σ(yi-f(xi))2→min
Простейшие виды интерп - линейная и квадратичная. При линейной точки заданной функции соединяются линейными отрезками, а при квадратичной - отрезками парабол.
Исп также кубическая сплайн интерполяция. Сплайн - модель гибкого тонкого стержня из упругого материала, закрепленного в 2-х соседних узлах интерполяции с заданными углами наклона α и β, так чтобы потенциальная энергия стержня была min.
Регрессия - представление совокупности данных некоторой функции F(x).
15 Численный метод наименьших квадратов
Метод наименьших квадратов (МНК) обычно исп в двух контекстах: в регрессионном анализе, как метод построения моделей на основе зашумленных экспериментальных данных, при этом часто оценивается погрешность, с которой вычислены её параметры; МНК часто прим просто как метод аппроксимации, без какой-либо привязки к статистике. МНК применяется также для приближённого представления заданной функции другими функциями и оказывается полезным при обработке наблюдений.
Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай МНК. Сущность метода состоит в отыскании параметров модели, минимизирующих ее отклонение от точек исх временного ряда, т. е.
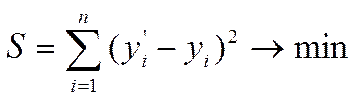 где y'i – расчетные значения исходного
ряда; уi –фактические значения исходного ряда; n – число
где y'i – расчетные значения исходного
ряда; уi –фактические значения исходного ряда; n – число
наблюдений. Если модель тренда представить в виде
y'=f(xi,a1,a2,…,ak,t) где a1,a2,...,ak – параметры модели; t – время; xi независимые переменные, то для того, чтобы найти параметры модели, удовлетворяющие условию S=… (выше). Пусть дано решить систему уравнений
a1x + b1y + c1z + … + n1 = 0;
a2x + b2y + c2z + … + n2 = 0; (1)
a3x + b3y + c3z + … + n3 = 0; … число которых более числа неизвестных x, у, z… Чтобы решить их по МНК, составляют новую систему уравнений, число которых равно числу неизвестных и которые затем решаются по обыкновенным правилам алгебры. Эти новые уравнения составляются по следующему правилу: умножают сперва все данные уравнения на коэффициенты у первой неизвестной х и, сложив полученное, получают первое нормальное уравнение, умножают все данные уравнения на коэффициенты у второй неизвестной у и, сложив полученное, получают второе нормальное уравнение и т. д. Если записать это кратко:
[aa] = a1a1 + a2a2 +…; [ab] = a1b1 + a2b2 +…; [ac] = a1c1 + a2c2 +…; …
[ba] = b1a1 + b2a2 +…; [bb] = b1b1 + b2b2 +…; [bc] = b1c1 + b2c2 +…; …
то нормальные уравнения представятся в следующем простом виде:
[aa]x + [ab]y + [ac]z + … + [an] = 0;
[ba]x + [bb]y + [bc]z + … + [bn] = 0 (2)
[ca]x + [cb]y + [cc]z + … + [cn] = 0; …
Коэфф. нормальных уравнений
весьма легко составляются из коэфф. данных, и притом коэфф. у первой неизв. во
втором уравнении равен коэфф. у второй неизв. в первом, коэфф. у первой неизв.
в третьем уравнении равен коэфф. у третьей неизв. в первом и т. д.
16. Функции интерполяции в аппроксимации в MathCad
Для интерполяции в MathCad надо чтобы точки xi были по возрастанию, не повторялись и для каждой была задана yi.
Линейная интерполяция linterp(vx,vy,x), где vx,vy - векторы координат узловых точек, x - значение аргумента, для которого будет получено интерполяционное значение y. Например yy(xx):=linterp(X,Y,xx) где xx задано xx:=0,0.01..10
Для проведения кубической сплайн интерполяции 3 встроенные функции
- cspline(vx,vy) - возвращ вектор вторы[ производных (vk), при приближении в опорных точках к кубическому полиному.
- pspline(vx,vy) - -//- к параболической кривой
- lspline(vx,vy) - -//- к приямой
Интерполирующая функция строится с пом interp(vk,vx,vy,x), x - произвольная точка, в которой выч значение интерполирующей функции.
xs:=0,0.01..10
s1:=lspline(X,Y)
sp1(xs):=interp(s1,X,Y,xs)
Можно проводить линейную регрессию общего вида в которой аппроксимирующая функция задается линейной комбинацией функций, при чем сами функции fi(x) могут быть нелинейными
f(x,k1,...,kn)=k1*f1(x)+...+kn*fn(x)
Линейная регрессия общего вида linfit(vx,vy,F) - функция аппроксимации по методу наименьших квадратов. Результат - вектор коэфов k, при котором среднеквадратичн погрешность приближения исходных точек с координатами vx, vy - min. Вектор F содержит функции fi(x), записанные в символьном виде.
Полиномиальная регрессия позвол аппроксимировать полином произвольной степени. Вычисление коэф полинома осущ с пом встроенной функц regress(vx,vy,n), n - степень полинома.
Для вычисления нелинейной регрессии общего вида надо определить параметры произвольной аппроксимир функ и применить genfit(vx,vy,vs,F) - возвращ вектор K параметров функции. Вектор vs задает начальные приближения элементов вектора K, рассчитываемые итерационным способом. Вектор F - искомая функция и ее частные производные по параметрам Ki в аналитическом виде.
Аппроксимация с помощью функций:
- expfit(x1,y1,vy), vy - начальные приближения, исп например для y=a*eb*x+с
- logfit(x1,y2,vy) для например y=a*ln(x+b)+с
- sinfit(x1,y2,vy) для например y=a*sin(x+b)+с
17. Численные методы решения ОДУ и систем ОДУ.
Численные методы решения ДУ исп при моделировании динамических тех объектов:
- метод последовательных приближений
- конечно-разностные методы, - Рунге-Кутта, - прогноза и коррекции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.