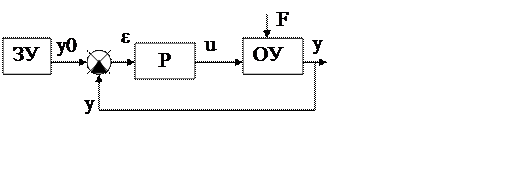
Корректирующее устройство еще называется регулятор.
Если e>0, то регулятор формирует управляющее воздействие u(t),
действующее пока не обеспечится e=0 или y=y0. Т.к. на регулятор подается разность сигналов, то
такая обратная связь - отрицательная, в отличие от положительной
ОС, когда сигналы складываются.
Недостаток: инерционность системы.
Поэтому часто применяют комбинации 2-х принципов: принцип обратной связи + принцип компенсации.
В завис от принципа и закона функционир ЗУ, задающего прогу изменения вых величины различают виды САУ: системы стабилизации, программные, следящие, самонастраивающиеся системы (экстремальные, оптимальные, адаптивные).
В системах стабилизации обеспечивается неизменные значения управляемой величины при всех видах возмущения, т.к. y(t)=const.
В программных системах. Обеспечивается изменение управляемой величины в соответствии с программой формируемой ЗУ.
Следящие системы отличаются от программных тем, что y=f(t) заранее неизвестно
В самонастраивающихся системах ЗУ ищет такое значение управляемой величины, которое в каком-то смысле является оптимальным.
Режим работы САУ в котором управляемая величина и в промежуточные величины не изменяются во времени- статические, но есть и динамические.
Процессы в динамическом режиме
1. Колебательный затухающий процесс
2. Незатухающий колебательный процесс
3. Расходящийся колебательный процесс.
В ТАУ часто используется операторная форма задания диф. уравнения.
При этом вводится ис.. дифференциального оператора
P=d/dt, так что dy/dt=py,а pu=du/dt.
Уравнение динамики можно записать в виде:
y=(b0*pm + b1*pm-1 +…+ bm)/( a0*pn + b1*pn-1 +…+ an) = K(p)/D(p) = W(p)*u
Дифференциальный оператор ω(p)- передаточная функция.
ω(p)=y(t)/u(t)- динамич. коэф усилия. Знаменатель передаточной функции D(p) называют характеристический полином.
Его корни, т.е. значения p, при котором знаменатель η(p) обращается в ноль, а ω(p) стремится к ∞, полюсы передаточной функции.
Числитель K(p)- операторный коэфф. передачи.
Его корни, при которых К(p)=0 и ω(p)=0 - нули. передаточной функции.
Передаточная ф-ия - основная хар-ка звена в динамическом режиме, из которой можно получить все остальные характеристики. Она представляется только параметрами системы и не зависит от входных и выходных величин.
41. Типовые звенья САУ, их переходные характеристики
Зависимость изменения вых величины сист. от времени при подаче на её вход единичного ступенчатого воздействия при нулевых начальных условиях - переходная хар-ка u(t). Импульсно переходная хар-ка K(t) опис реакцию сист на одиночное импульсное воздействие при нулевых начальных условиях. Единичный импульс физически представляет из себя очень узкий импульс, ширина которого стремиться к нулю, а высота к ∞, ограничивающий единичную площадь. Математически он описывается дельта функцией d(t)=l(t).
Переходная и импульсные характеристики - временные хар-ки. Типы звеньев:
Усилительное (пропорциональное, безинерционное) звено (трансформатор). Это звено для которого в любой момент времени выходная величина пропорциональ-на входной. Его уравнение: y(t)=K(t)u(t). K(t)- коэфф. усиления, К(t)=K=const- звено стационарное. Передаточная функция: ω(p)=K
В ответ на единичные ступенчатые воздействие сигнал на выходе мгновенно достигает величины в K раз >, чем на входе и сохраняет это значение.
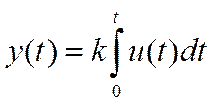При K=1
звено никак себя не проявляет, а при К=-1- инвертирует вх значение.
Интегрирующее(астатическое) звено или dy/dt = ku. Выходной
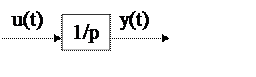сигнал
получается в результ интегрирования входного сигнала. Передаточная функция: ω(p)=K/р.
При К=1 звено представляет собой
чистый интегратор ω(p)=1/р.
Дифференцирующее звено. Различают идеальное и реальное диф. звено. Уравнение динамики идеального звена: y(t) = k(du/dt) или y=Kpu
Здесь выходная величина пропорциональна скорости изменения вх величины.
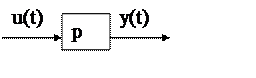Передаточная
функция: ω(p)=Kр. При К=1 звено осущ чистое дифференцирова-ние ω(p)=р.
Идеальное диф. звено реализовать невозможно.
Апериодическое звено первого порядка (инерциальное) (электродвигатель)
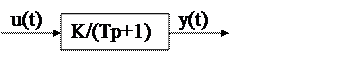Уравнение
динамики: T(dy/dt)+y = ku или Tpy+y=ku Передаточная функция: W(p) = K/Tp+1
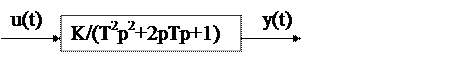Апериодическое
звено 2-го порядка T12*p2*y = T2*p*y+y=Ku Передаточная функция: W(p) = K/(T12*p2 + T2*p +1) Решение уравнения зависит от соотношения времени
T1 и T2, которое определяет коэффт затухания: r=T2/T1 W(p) = K/(T2*p2 + 2pTp
+1), где Т=Т1.
Если r>=1, то знаменатель ω(p) имеет 2 вещественных корня р1 и р2, и раскладываются на 2 сомножителя. Если r<1 корни знаменателя ω комплексно сопряженные: P1,2=a ± jw Такое звено – колебательное.
Переходная хар-ка - выражение, характеризующее затухающий колебательный процесс с затуханием а и частотой ω. Например: колебательный контур.
Реальное дифференцирующее звено Tpy + y=1+Tpy Передаточная функция: w(p)=KTp/Tp+1
42. Соединение структурных звеньев САУ
3 вида соединения структурных звеньев:
-последовательное
-параллельное
-с обратной связью
1. последовательное соединение- выходная величина предшествующего звена попадают на вход последующего.
Цепочка последовательного соединения звеньев преобразуется в эквивалентное звено с передаточной функцией, = произвед. передаточных функций отдельных звеньев.
W(S) = W1(S) *
W2(S)
2. Параллельное соединение (согласное)- на вход каждого звена подается один и тот же сигнал, а выходные сигналы складываются.
Цепочка звеньев, соединенных параллельно, преобразуется в звено с передаточной функцией, равной сумме передаточных функций отдельных звеньев
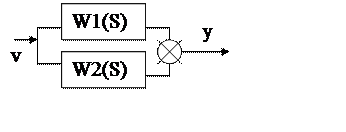W(S) = W1(S)
+ W2(S)
3.Соединение с обратной связью
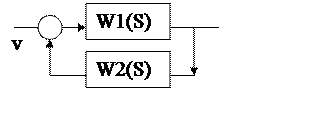W(S) = W1(S)/(1 ± W1(S) - W2(S))
43. Частотные характеристики САУ
Если подать на вход системы с передаточной функцией ω(p) гармонический сигнал
u(t) = Umejωt = Um (cos ωt + jsinωt)
То после завершения переходного процесса на выходе установится гармонические колебания
y(t) = Ymej(ωt+φ) = Ymejωt ejφ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.