Зависимости, связывающие амплитуду и фазу выходного сигнала с частотой входного сигнала, называются частотными характеристиками (ЧХ).
Анализ ЧХ системы с целью исследования её динамических свойств - частотный анализ.
Уравнение динамики в частотном виде:
y=((b0*(jω)m + b1*(jω)m-1 +…+ bm)/( a0*(jω)n + b1*(jω)n-1 +…+ an) ) *u = W*(jω)
ω(j ω)- частотная передаточная функция получается заменой р на jω.
ω(j ω) =A* ω* ejφ(ω) = p (ω)*jQ(ω)
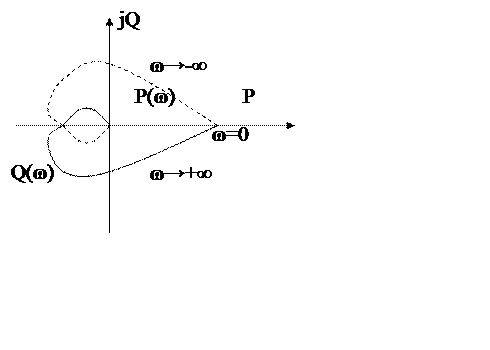 А(ω)-
амплитудная.
А(ω)-
амплитудная.
Если ω(j ω) изобразить вектором на комплексной плоскости, то при изменении ω от 0 до +∞ конец вектора будет вычерчивать кривую, называющуюся годографом вектора ω(j ω), или амплитудную фазовую частотную арку (АФЧК)
44. Устойчивость линейных динамических систем
Аксиома1: устойчивость определяется внутренним состоянием ДС.
Аксиома2: устойчивость не является абсолютным свойством ДС.
Метод оценки устойчивости ЛДС по корням характеристического уравнения.
Диф. уравнение => характеристич. уравнение => корни.
Корни в общем виде: r1,2 = ±a±jw
-Если корни вещественны и отрицательны, то система- устойчивая без колебаний.
-Если комплексное (-с+jω) с отрицательной вещественной частью- устойчивая с колебаниями.
-Один из корней равен 0- нейтральная.
-Корни мнимые – система на границе устойчивости (незатух. колеб).
-Корень вещественный положительный - неустойчивая.
-Корни комплексные с (+а)- КДС неустойчива (колебания).
Для устойчивости системы необходимо и достаточно, чтобы корни характеристич ур-ния имели отрицательные действительные части, т. е. располагались в левой полуплоскости комплексной плоскости. Если система устойчива, то все коэффициенты характеристического уравнения имеют одинаковое значение.
45. Общая характеристика пакета Control System Toolbox
Пакет Control System Toolbox предназначен для исследования линейных стационарных систем (ЛСС) методами теории автоматического управления.
В пакете реализованы:
-полный набор средств для анализа одномерных и многомерных ЛСС
-временные характеристики: передаточная и переходная функции, реакция на производные входные воздействия
-частотные характеристики: диаграммы Боде, Найквиста
-разработка замкнутых систем регулирования
-проектирование регуляторов.
В состав пакета включены более 100 функций.
Пакет построен по объектно-ориентированному признаку и включает следующие классы:
-Родительский объект (класс) –LTI (Line-Time-Invariant System- ЛСС)
-Дочерние объекты:
-tF- объект (Transfer Function- передаточная функция)
-zpK- объект(Zero Pole Gain)
-ss – объект (State Spane- Пространство состояния)
Объект LTI содерж инфу, не зависящую от конкрет представления и типа ЛСС.
Дочерние объекты определяются конкретной формой представления ЛСС.
tF- объект- характеризуется векторами коэфов полиномов числителя и знаменателя рациональной передаточной функции.
zpK- характеризуется векторами, которые содержат значения нулей и полюсов передаточной функции системы, а также коэффициент передаточной системы.
ss- определяется 4-мя матрицами, описывающими динамическую систему в пространстве состояний.
Пакет Control System Toolbox обеспечивает создание структуры данных для модели любого из перечисленных видов объектов в форме массива ячеек, не зависящих от конкретного представления модели.
Это позволяет манипулировать линейной системой как единым объектом, а не набором данных в виде векторов и матриц.
46. Функции пакета для создания LTI-моделей
Создание модели в виде передаточной функции.
Общий вид: Sys= tf(nom,den)
nom и den- векторы-строки коэффициентов полинома числителя и знаменателя передаточной функции, расположенных в порядке убывания степеней.
H(S) = S/(S2+2*S+10) Команда м-файла H1=tf([1 0],[1 2 10]).
Если это последовательное соединение 2-х звеньев, то передаточная функция определяется следующими командами: =series(H1,H2) или H=H2*H1
Параллельное соединение: H=parallel(H1,H2) или H=H2+H1
Соединение с обратной связью: передаточная функция замкнутой системы определяется выражением: H=feedback(H1,H2).
При положительной обратной связи команда: H=feedback(H1,H2,+1)
Пример получения передат фу-и системы с единичной ООС: W1=K1/(T1*S+1)
 W2=K2/S W3=(T3*S+1)/(T4*S+1)
W2=K2/S W3=(T3*S+1)/(T4*S+1)
М-файл:
w1=tF([K1],[T1 1]) w2=tF([K2],[ 1 0])
w3=tF([T3 1],[T4 1])
w4=w1*w2+w3 //послед-парал соед
w5=1 //единичная обратная связь
w6=Feedback(w4,w5)
Извлечение данных из модели выполняется функцией tFdata:
Общий вид: [num,den]=tfdata(sys) num, den- результаты работы функции: числитель и знаменатель передаточной функции. Например H1=tf([1 0],[1 2 10])
step(LTI-объект) - построение графика перех процесса (реакция на ступенч сигн)
[y,t,x]=step(lti-объект)- получение векторов перех процесса, переменных состояния и моментов времени, при этом график перех процесса не отображается.
Команда [y,t,x]=step(H1) приводит к формированию векторов y и t, по которым с помощью команды plot(t,y) можно построить график перех процесса.
Ф-ия bode для получ диаграммы Боде (графиков логарифмических АЧУ и ФЧХ)
Общий вид: bode(lti- объект) – построение диаграммы Боде заданного объекта.
[A,PH,w]=bode(lti- объект) получение векторов амплитуды, фазы и частоты.
Функция nyquist для получения диаграммы Найквиста (годографа) Общий вид:
Nyquist(lti-объект)- построение диаграммы Найквиста заданного объекта.
[Re,lw,w]=nyquist(lti-объекта)- получение вектора вещественной и мнимой частей комплексного коэффа переданного для задания набора частот и вектора частот.
Для вычисления полюсов модели исп команда: Pole(lti- объекта) P=pole(H1) Приведет к получению вектора характеристического ур-ия.
Для вычисления нулей модели исп zero(lti-объекта) или [z,gain]=zerо(lti- объект).
Ф-ия, вызванная в виде zero(lti), еще возвращает и обобщенный коэфф усиления.
Функция pzmap для получения карты нулей и полюсов модели. Pzmap(lti) и [p,z]=pzmap(lti) При применении последней формы графики не выводятся, а формируются векторы полюсов и нулей модели.
47. Моделирование LTI-моделей в Simulink
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.