Метод Рунге–Кутта
Применяется для решения ДУ из-за высокой точности.
Отличительная особенность — уточнение наклона интегральной кривой за счет вычисления производной не только в начале текущего отрезка интегрирования, но и, например, в середине отрезка (для двучленных схем Р–К) или 4хкратное вычисление производных в методе 4ого порядка. При одном уравнения двучленная итерационная формула:
yn+1=yn+hf(xn+0,5h,yn+0,5hfn)
Последовательность вычислений: сначала делают половинный шаг по схеме ломаных (по формуле Эйлера), находя yn+0,5=yn+hy’n+0,5, затем в найденной точке определяют наклон кривой y’n+0,5=f(xn+0,5, yn+0,5) и по этому наклону определяют приращение на целом шаге yn+1=yn+ hy’n+0,5.
Четырехчленная схема Рунге–Кутта наиболее часто употребляется в машинных расчетах и имеет четвертый порядок точности:
yn+1=yn+(h/6)*(k1+2k2+2k3+k4)
k1=f(xn,yn); k2=f(xn+h/2,yn+hk1/2),
k3=f(xn+h/2,yn+hk1/2), k4=f(xn+h,yn+hk3),
Метод Рунге–Кутта легко переносится и на случай системы ДУ.
Метод конечных разностей
Широко известный и простейший метод интерполяции. Его суть заключается в замене дифференциальных коэффициентов уравнения на разностные коэффициенты[1], что позволяет свести решение дифференциального уравнения к решению его разностного аналога, т.е. построить его конечно-разностную схему.
Так, заменив производную в обыкновенном дифференциальном уравнении
u'(x) = 3u(x) + 2
на конечную разность
(u(x+h)-u(x))/h ≈ u’(x),
получаем аппроксимированную форму (конечно-разностную схему)
u(x+h) = u(x) + h(3u(x)+2).
Последнее выражение носит название конечно-разностного уравнения, а его решение соответствует приближённому решению первоначального дифференциального уравнения.
20. Определение, виды и п-ры динам модели, понятия времени, прост-ва, дв.
Динамическая модель – система, зависящая от времени. Ньютон различал: физическое (астрономическое ) время, математическое (абсолютное) – без конкретной привязки к чему-либо внешнему, непрерывное, дискретное – возрастающая последовательность вида {t1,t2,…,t3}. Дискретное время прим там, где наблюдается разделение технического объекта на «быстрое» и «медленное». Графики функций x(t),y(t),z(t) – временные диаграммы.
С позиций классической физики наше пространство рассматривается как трехмерное, однородное и изотропное, не зависящее от находящихся в нем материальных тел и подчиняющееся евклидовой геометрии. Ньютон подразумевал два вида пространства: относительное, с которым люди встречаются путем измерения пространственных соотношений между телами, и абсолютное - пустое вместилище тел, трехмерное евклидово пространство, то есть фактически различал пространство движения и движение в пространстве.
По видам оператора (глобальной функции) динамические системы и их модели делятся на: линейные и нелинейные, непрерывные и дискретные, стационарные и нестационарные, одномерные и многомерные, с сосредоточенны-ми и распределенными параметрами.
Линейные системы - описываются линейными диф. урами
Нелинейные системы - описываются нелинейными диф. уравнениями
Непрерывные системы - описываются диф. урами.
Дискретные – описываются разностными диф урами.
Стационарные системы – описываются уравнениями с постоянными коэф.
Нестационарные системы - описываются уравнениями с переменными коэф.
Одномерные системы – имеют один вход – один выход.
Многомерные системы – имеют суммарное число входов и выходов ≥2.
Внешние воздействия делятся на:
1. Непрерывные (функция непрерывного аргумента).
2. Дискретные (функция дискретного аргумента).
3. Детерминированные и случайные.
4. Одномерные и многомерные.
Например, динамическая система описывается диф. уравнением вида:
an(t)∙(dnx(t))/dtn+...+a0(t)x(t)=bm(t)∙(dmy(t))/dtm +...+b0(t)y(t) здесь:y(t) – входной
сигнал, x(t) – выходной сигнал, a(t), b(t) – внутренние параметры системы, коэфы левой и правой частей уравнения. Эта система: линейная, непрерывная, нестационарная, детерминированная, одномерная. Внешние воздействия: непрерывные, детерминированные, одномерные. Если коэффициенты уравнения постоянные, то система называется линейной стационарной:
an(dnx(t))/dtn+...+a0x(t)=bm(dmy(t))/dtm +...+b0y(t)
Для механических систем основными выходными параметрами являются:
- зависимость перемещения (линейного, углового) от времени
- зависимость ускорения от времени
- зависимость скорости от времени
21. Формы представ и методы реализ динам моделей. Виды внешних воздейс
Динамическая модель может быть представлена в следующих формах:
– Явная функция, зависящая от времени z=z(t)
– Нелинейное алгебраическое уравнение относительная переменных явно зависящих от времени G(z(t),t)=0
– Диф. уравнение или система
– Алгебраическое диф. уравнение
– Интегро-диф. уравнение или система
– Передаточная функция
Один из методов реализации динамических - с использованием передаточной функции.
Внешние воздействия делятся на:
– Непрерывные (функция непрерывного аргумента).
– Дискретные (функция дискретного аргумента).
– Детерминированные и случайные.
– Одномерные и многомерные.
Входные воздействия описываются различными функциями, в том числе и обобщенными. Выделяют 3 типа воздействия: импульсивное, единичная ступенчатая функция, гармоническое воздействие.
|
 |
δ -
функция (или функция Дираки,
единичная импульсная функция) позволяет записать пространственную плотность
физической величины сосредоточенной или приложенной в одной точке
Функция Хэвисайда - первообразная функция для δ – функции Дирака, Н` = δ
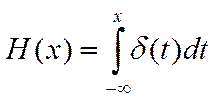Гармоническое воздействие (колебание) – явление
природного периодического изменения какой-либо величины, при кот зависимость от
аргумента имеет характер функции sin или cos
Полный вид: x=A*sin(или cos)(ωt+φ)
22. Интегральное преобразование Лапласа
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.