Линейные цепи постоянного тока в установившемся режиме. Линейные цепи переменного тока в установившемся режиме. Трехфазные цепи в установившемся режиме. Расчет линейных цепей в переходном режиме

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

“Новгородский государственный университет имени Ярослава Мудрого”

______________________________________________________________________

Кафедра "Промышленная энергетика"

РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Контрольная работа по дисциплине

«Электротехника и электроника: Общая электротехника и электроника»

Вариант 10

Преподаватель              

_______________

Подпись                                                       

«____» _________2009 г.

Студент гр.                    6411з          

_______________

Подпись                                                       

«____» _________2009 г.

Содержание

стр.

1. Линейные цепи постоянного тока в установившемся режиме

Задача №1                                                                                                       3

2. Линейные цепи переменного тока в установившемся режиме

Задача №2                                                                                                       16

Задача №3                                                                                                       22

3. Трехфазные цепи в установившемся режиме

Задача №4                                                                                                       33

4. Расчет линейных цепей в переходном режиме

Задача №5                                                                                                  41

5. Литература                                                                                             44

КОНТРОЛЬНЫЕ ЗАДАНИЯ

1. Линейные цепи постоянного тока в установившемся режиме

Задача 1

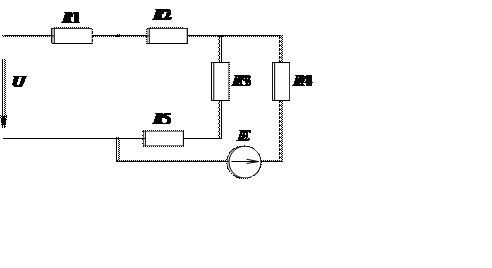
Определите токи в ветвях цепи постоянного тока и напряжения на её элементах. Правильность расчета подтвердите составлением баланса мощностей. Схема цепи представлена на рисунке 1.1. Значения параметров элементов цепи указаны в таблице 1.1. Расчет выполните всеми перечисленными методами:

1) метод непосредственного применения законов Кирхгофа ,

2) метод структурных преобразований цепи

-  при условии Е=0,

-  при условии U=0

3) метод наложения,

4) метод эквивалентного генератора (постройте график изменения тока в одной из ветвей в зависимости от величины сопротивления резисторов этой ветви).

Рисунок 1.1

Таблица 1.1

Е, В	U, В	R1 ОМ	R2 ОМ	R3 ОМ	R4 ОМ	R5 ОМ
95	145	22	42	14	55	26

1) Решение задачи методом непосредственного применения законов Кирхгофа

Представим схему изображенную на рисунке 1.1 в следующем виде:

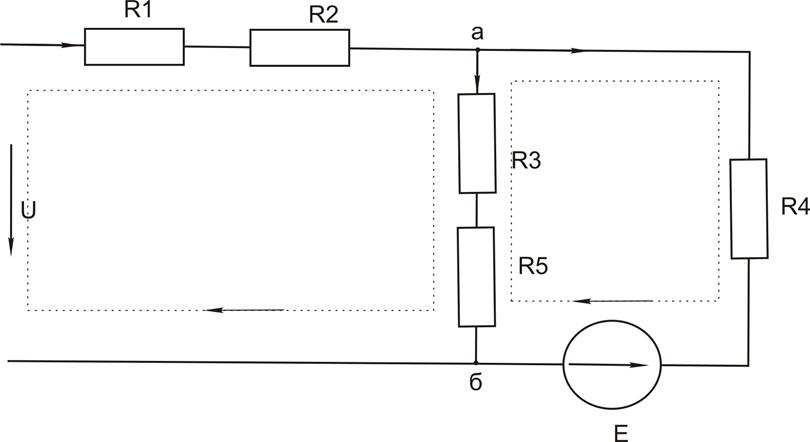
Рисунок 1.2

Схема замещения имеет два узла, три ветви и два независимых контура на рисунке обозначенных пунктиром. Составим для узла «а» уравнение по первому закону Кирхгофа:

I - I₃ - I₄ = 0                                                                                            (1.1)

Для независимых контуров по второму закону Кирхгофа, уравнение имеет вид:

IR₁ + IR₂ + I₃R₃ + I₃R₅ – U = 0                                                              (1.2)

I₄R₄ – I₃R₅ – I₃R₃ = - E                                                                           (1.3)

В результате получим систему уравнений:

I - I₃ - I₄ = 0                                         

IR₁ + IR₂ + I₃R₃ + I₃R₅ – U = 0                                                              (1.4)

I₄R₄ – I₃R₅ – I₃R₃ = - E

Преобразуем систему (1.4) так, чтобы в ней присутствовали неизвестные токи ветвей.

I – I3 – I4 = 0

I(R₁ + IR₂)+ I₃(R₃ + R₅) = U                                                                  (1.5)

I₄R₄ – I₃(R₃ +R₅) = - E

Решим систему уравнений (1.5) методом подстановки, для чего из второго уравнения системы найдем ток I:

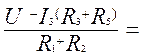
I =   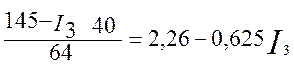                                       (1.6)

Из третьего уравнения находим ток I₄:

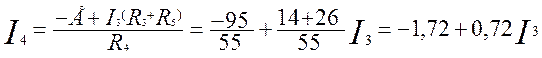                                  (1.7)

Определим ток I3 подставив значения (1.6) и (1.7) в уравнение (1.1)

2,26 – 0,625I₃ – I₃ + 1,72 – 0,72I₃ = 0

I₃ + 0,625I₃ + 0,72I₃ = 2,26 + 1,72

I₃ = 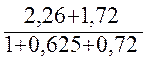= 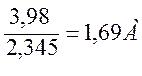                                                            (1.8)

Из выражения (1.7) найдем ток I₄:

I₄ = -1,72 + 0,72·1,69 = -0,5А                                                               (1.9)

Подставив в уравнение (1.6) значение I₃, найдем ток I:

I=2,26 – 0,625∙1,69 = 1,2А                                                                    (1.10)

Найдем напряжения в цепи, воспользовавшись моделью идеального резистора:

U₁ = IR₁ = 1,2·22 = 26,4 В                                                                    (1.11)

U₂ = IR₂ = 1,2·42 = 50,4 В                                                                    (1.12)

U₃ = I₃R₃ = 1,69·14 = 23,66 В                                                               (1.13)

U₄ = I₄R₄ = - 0,5·55 = -27,5 В                                                               (1.14)

U₅ = I₃R₅ = 1,69·26 = 43,94 В                                                               (1.15)

Составляем баланс мощностей цепи:

UI – EI₄ = 145·1,2 – 95 (-0,5) = 221,5 Вт                                             (1.16)

Мощность потребляемая в цепи приемниками электроэнергии, равна сумме мощностей отдельных элементов цепи:

I²×(R₁ + R₂) + I₃(R₃ + R₅) + I₄²·R₄= 1,2²·64 + 1,69² 40 + (- 0,5)²·55 = 92,16 + 114,244 + 13,75 = 220,15 Вт                                                                           (1.17)

2) Решение методом структурных преобразований при условии,

что Е= 0

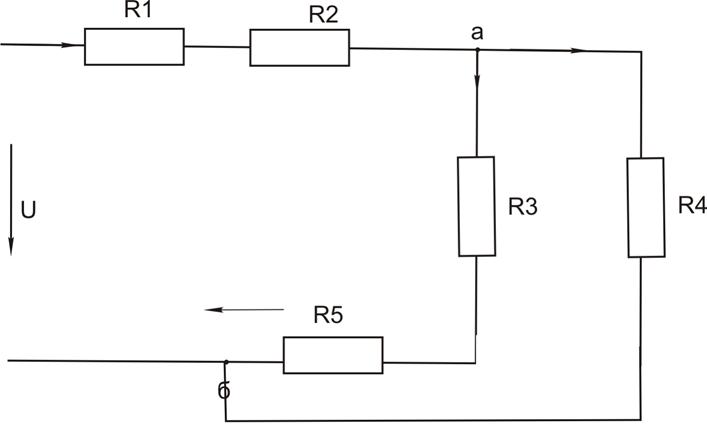
рисунок 1.3.

1. Положим Е = 0, тогда первое упрощение схемы выполним преобразовав ветвь из двух последовательно соединенных идеальных резисторов R₁ R₂ и R₃ R₅  рисунок (1.3) в соответствующую ветвь состоящую из резисторов R_1,2 и R_3,5 соответственно, рисунок (1.4):

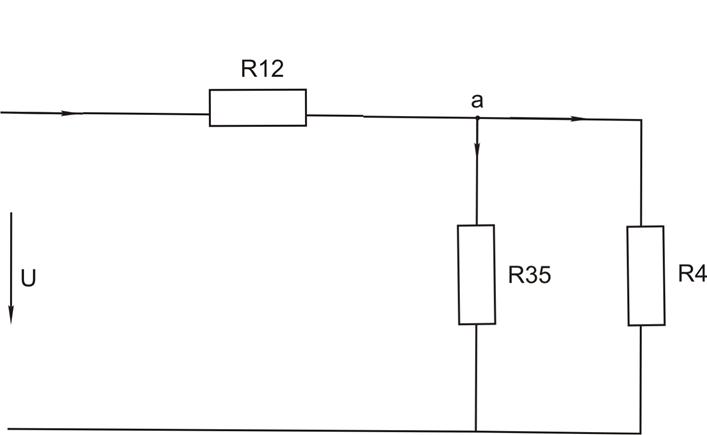
рисунок 1.4

2. Суммарное сопротивление эквивалентного резистора R12 равно сумме R1 и R2:

R₁₂ = R₁ + R₂ = 22 + 42 = 64 Ом                                                          (1.18)

Суммарное сопротивление эквивалентного резистора R35 равно сумме R3 и R3:

R₃₅ = R₃ + R₅ = 14 + 26 = 40 Ом                                                          (1.19)

3. Заменим две параллельно соединенные ветви R35 и R4 одной эквивалентной ветвью образованной резистором R354, схема примет вид:

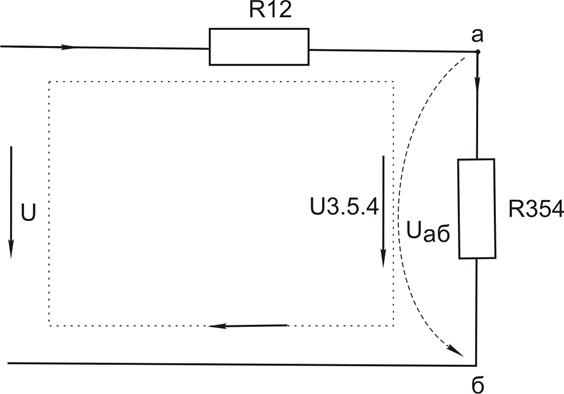
рисунок 1.5

Определим в этой схеме параметры всех элементов:

R₃₅₄ = 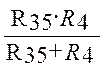= =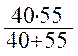23,15 Ом                                                     (1.20)

4. Запишем уравнение электрического состояния цепи, используя для этого второй закон Кирхгофа, и решим полученное уравнение относительно тока I: