Линейные цепи постоянного тока в установившемся режиме. Линейные цепи переменного тока в установившемся режиме. Трехфазные цепи в установившемся режиме. Расчет линейных цепей в переходном режиме, страница 3

I₃= I_3.1+ I_3.2 = 0,9545 + 0,731 = 1,685 A (1.50)

I₄= I_4.1– I_4.2= 0,6941 - 1,19 = - 0,495 A (1.51)

Значения найденных токов совпадают со значениями вычисленных напряжений по методу непосредственного применения законов Кирхгофа. Задача решена правильно.

4) Решение задачи методом эквивалентного источника.

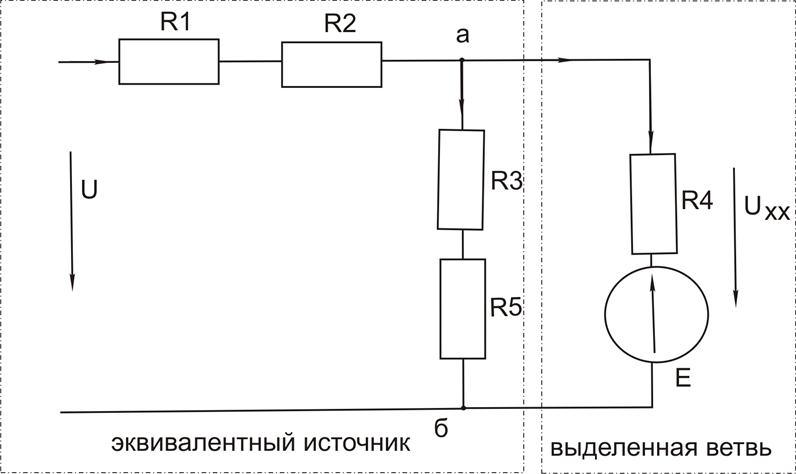
image description

Рисунок 1.11

Выделим ветвь, оставшуюся часть цепи будем рассматривать как некоторый эквивалентный источник тока. Расчет производим методом непосредственного применения законов Кирхгофа. Составим для узла «а» уравнение, используя первый закон Кирхгофа, последующие уравнения составляются используя второй закон Кирхгофа по отношению к таким двум независимым контурам, каждый из которых включал бы в себя выводы источника. Система уравнений имеет следующий вид:

I₁ – I₃ = 0

I₃(R₃ + R₅) – Uхх = 0 (1.52)

I₁(R₁ +R₂) + Uхх - U= 0

Из второго уравнения найдем ток I₃, а из третьего ток I₁:

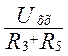I₃ = = (1.53)

I₁ = 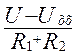==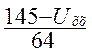 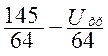(1.54)

Подставив найденные значения токов I₁ и I₃ в первое уравнение системы найдем Uхх:

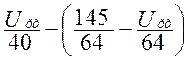=0 (1.55)

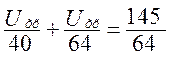
0,04Uхх = 2,265

Uхх = 56,64

Напряжение холостого хода эквивалентного источника равно его ЭДС:

Uхх = Еэu = 56,64 В

Теперь рассчитаем эквивалентный источник в режиме короткого замыкания. Схему изображенную на рисунке 1.12 преобразуем так чтобы выводы эквивалентного источника были соединены между собой – замкнуты.

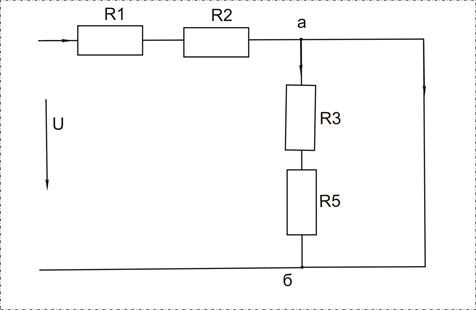
image description

рисунок 1.12

Источник напряжения U, создает частный ток Iк короткого замыкания.

I_к = I₁ =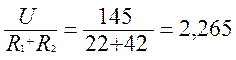A (1.56)

В нашем случае в электрической схеме один источник напряжения, поэтому ток Iк короткого замыкания равен току эквивалентного источника.

Iк = 2,265 А

Зная ЭДС эквивалентного источника и ток Iк короткого замыкания , найдем внутреннее сопротивление эквивалентного источника рисунок 1.13

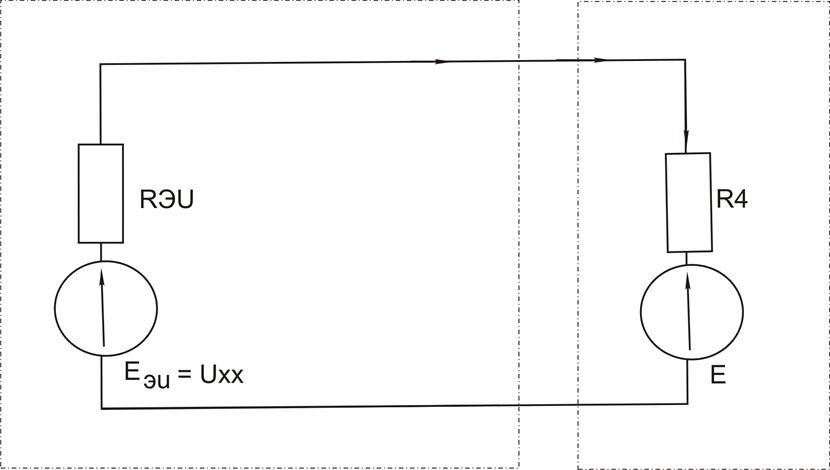
image description

Рисунок 1.13

Найдем R_эu = 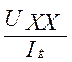= 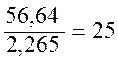Ом (1.56)

Определим ток I₄ применив второй закон Кирхгофа:

I₄ = 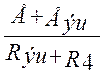(1.57)

Подставив Rэu в формулу (1.57) значение тока I₄:

I₄ = 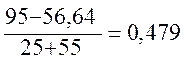А

Задача определения тока в одной ветви решена. График изменения тока I₄ в зависимости от величины сопротивления (R4) выделенной ветви рисунок 1.14

R₄ Ом	0	10	20	30	40	50	60	70	80
I₄ A	1,53	1,09	0,85	0,69	0,59	0,51	0,45	0,4	0,36

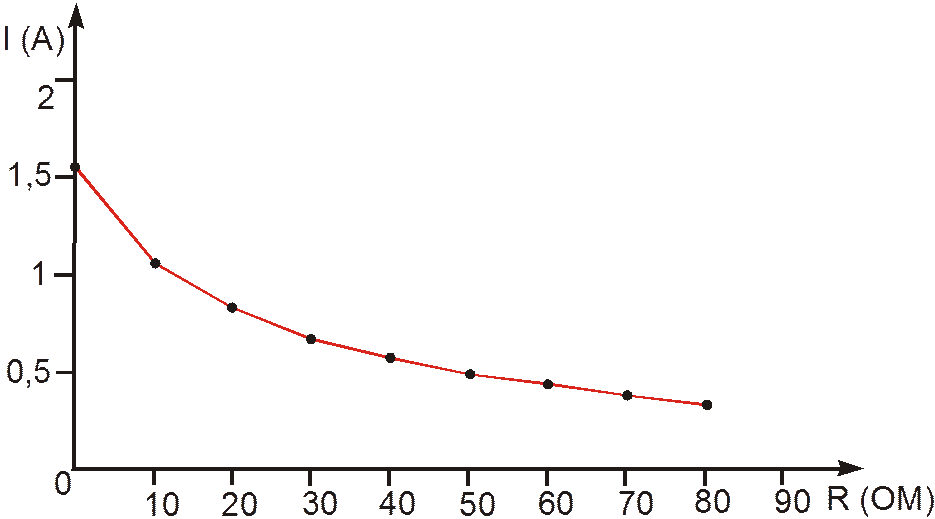
Рисунок 1.14

2. Линейные цепи переменного тока в установившемся режиме.

Задача 2. Руководствуясь графиками синусоидально изменяющихся токов i₁ … i₅, приведенными на рисунке 2.1, определите для каждого из токов его частоту, угловую частоту, амплитуду, действующее значение, мгновенное значение при t = 0,01 с, а также начальную фазу.

Рисунок 2.1

Представьте токи, в виде

- тригонометрических функций,

- комплексной алгебраической форме записи,

- комплексной показательной форме записи.

Найдите комплексные амплитуды токов. Изобразите токи векторами комплексных действующих значений.

1. Определяем частоты токов f - частота, это количество полных колебаний в секунду или f = (2.1)

T₁ = 0,02c = f₁ = = = 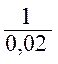50 Гц (2.2)

T₂ = 0,02c = f₂= ==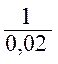50 Гц (2.3)

T₃ = 0,02c= f₃= ==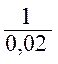50 Гц (2.4)

T₄ = 2, определяем время одного периода, из рисунка 2.1 находим цену одного деления 1/600 сек. Период повторения синусоидального изменяющегося тока i₄ Равен 16. следовательно можно найти f₄:

f₄= 600/16 = 37,5 Гц или (2.5)

T₅ = 0,02с = f₅ =1/T₅ = 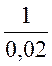= 50 Гц (2.6)

2. Определяем угловую частоту

Угловой (циклической) частотой синусоидально изменяющейся величины тока i, называется величина ω, показывающая скорость изменения фазы во времени. Зависимость частоты тока и угловой частоты определяется из формулы f = (2.7)