Изобразим схему в более удобном виде
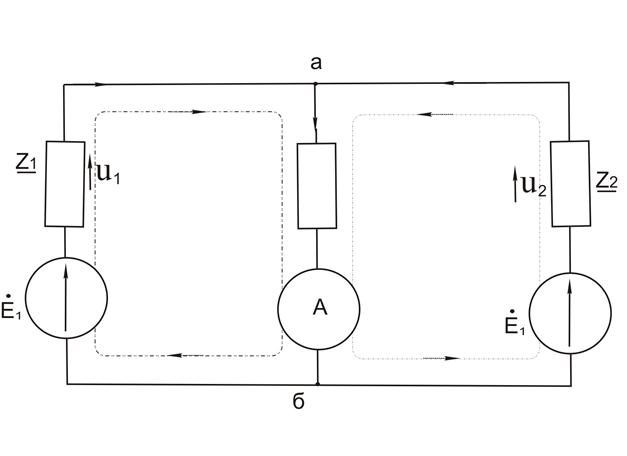
рисунок 3.2
Для узла «а» составим уравнение по
первому закону Кирхгофа
İ1+İ2-I3=0
Z 1×İ1+Z 3×İ3=E1 (3.1)
Z 2×İ2+Z 3×İ3=E2
Получили систему уравнений, из второго уравнения найдем ток İ1:
İ1=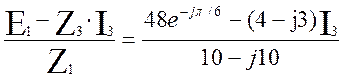
= (3,26+j0,86)-(0,35+j0,05) İ3 А (3.2)
Из третьего уравнения найдем ток İ2:
İ2=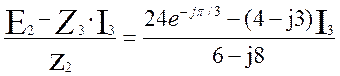
= (2,37+j0,27)-(0,48+j0,14) İ3 А (3.3)
Подставим полученные выражения токов İ1 и İ2 в первое уравнение системы (3.1) и найдем значение тока İ3
İ3=(3,26+j0,86)-(0,35+J0,05) İ3+(2,37+j0,27)-(0,48+j0,14) İ3 (3.4)
5,63+j0,59=1,83I3 +j0,19I3
5,63+j0,59=I3(1,83+j0,19)
I3=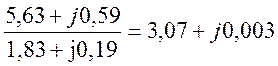
Теперь найдем значение токов İ1 и İ2
İ1=(3,26+j0,86)-(0,35+J0,05)(3,07+j0,003)=2,19+j0,71 A (3.5)
İ2=(2,37+j0,27)-(0,48+j0,14)(3,07+j0,003)=0,9-j0,7 A (3.6)
Зная значения токов, найдем искомые напряжения:
Ū1=Z1·İ1=(10-j10)(2,19+j0,71)=29-j14,8 B (3.7)
Ū2=Z2·İ2=(6-j8) (0,9-j0,7)=-0,2-j11,4 B (3.8)
Ū3=Z3·İ3=(4-j3) (3,07+j0,003)=12,28-j9,19 B (3.9)
Показания амперметра:
А=İ3=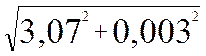
=3,06 А (3.10)
2) Решение задачи методом наложения
На рисунке 3.3 изображена электрическая схема представляющая собой совокупность схем замещения.
|
|
Оставим один источник ЭДС Е1 и изобразим схему замещения на рисунке 3.4, обозначив напряжения и токи элементов схемы двумя индексами: - первый – ток и напряжение в исходной схеме замещения; - второй – номер источника в рассматриваемой частной схеме. |
Рисунок 3.3
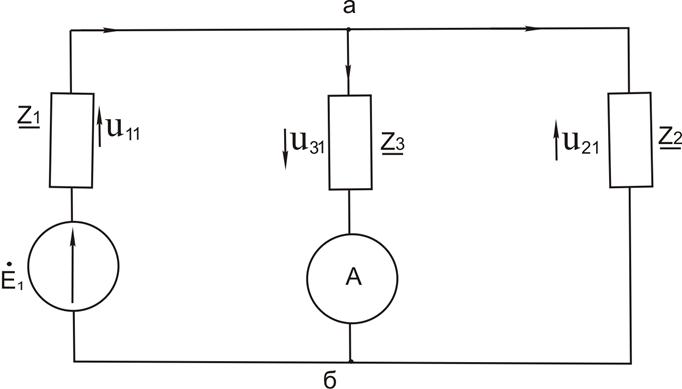
Рисунок 3.4
Расчет схем производится методом структурных преобразований, заменим две параллельные ветви – одной эквивалентной ветвью образованной новым элементом Z23 рисунок 3.5. Найдем полное комплексное сопротивление новообразованной ветви.
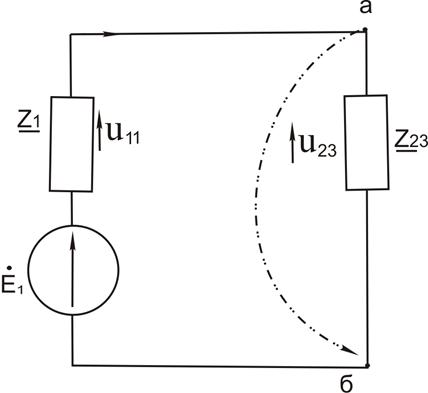Рисунок
3.5
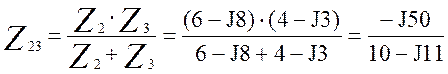=2,48-J2,26
Ом (3.11)
В соответствии со вторым законом Кирхгофа найдем ток I11
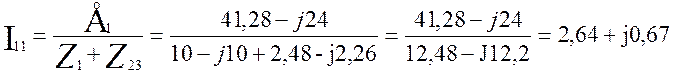A (3.12)
Зная ток I11, найдем напряжение Ūаб1:
Ūаб1=Ū23 İ11= Z23 İ11=(2,48-j2,26)·(2,64+j0,67)=8,06-j4,3 B (3.13)
Теперь необходимо найти токи I21 и I31
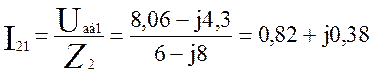A (3.14
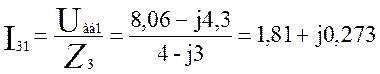A (3.15)
Заменим источник и изобразим частную схему замещения с ЭДС Е2 рисунок 3.6
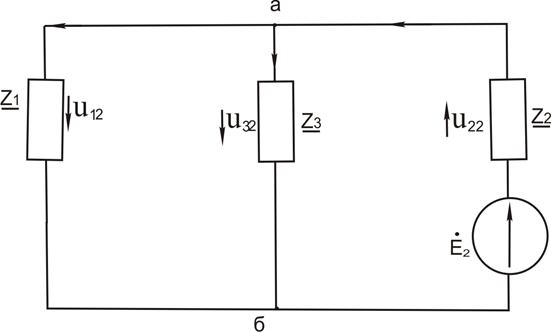
Рисунок 3.6
На схеме замещения заменим две параллельные ветви одной эквивалентной ветвью образованной новым элементом Z13 рисунок 3.7
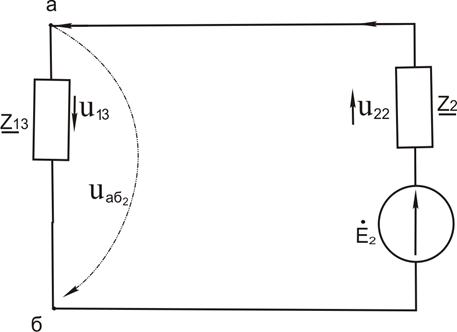
Рисунок 3.7
Полное комплексное сопротивление этой ветви равно:
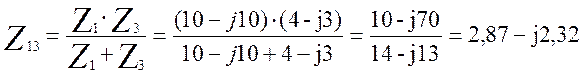(3.16)
В соответствии со вторым законом Кирхгофа найдем ток I22:
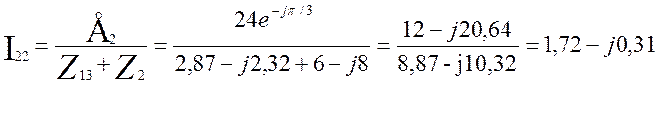(3.17)
Найдем напряжение Ūаб2 по известному I22 и Z13:
Ūаб2=Ū13= Z13 İ22=(2,87-j2,32)(1,72-j0,31)=4,21-j4,88 (3.18)
Теперь найдем токи I12 и I32:
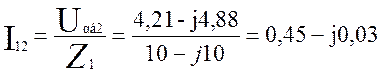(3.19)
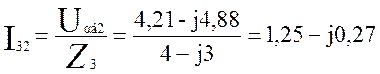(3.20)
Просуммировав значения частных токов в комплексной форме с учетом их направлений, рисунок 3.2 получим значения искомых токов во всех ветвях рассматриваемой цепи.
(3.21)
(3.22)
(3.23)
Сравнивая данные значения токов со значениями, полученными при решении задачи методом непосредственного применения законов Кирхгофа, видим, что с учетом погрешности данные значения совпадают. Задача решена правильно.
Выражение баланса мощности в электрической цепи находится как равенство сумм комплексных мощностей всех источников суммарной комплексной мощности всех приемников.
ΣKЕKIK=ΣnUnIn (3.24)
Где IK и IK – сопряженные комплексные токи K - го источника и n - го приемника. Сопряженный комплексный ток для источника Е1 равен току:
I1 = I1 = 2,19 + J0,71 (3.25)
Сопряженный комплексный ток для источника Е2 равен току:
I2 = I2 = 0,9 – J0,7 (3.26)
Подставим найденные параметры в выражение (3,24) и определим суммарную мощность источников и суммарную мощность приемников:
ΣKЕKIK= Е1I1+ Е2I2=(41,28-j24)(2,19+j0,71)+(12-j20,64)(0,9-j0,7)=
=(107,44-j23,25)+(-3,64-j26,97)=103,79-j50,22
ΣnЕnIn=U1I1+U2I2+U3I3=(29-j14,8)(2,19+j0,71)+(-0,2-j11,4)(0,9-j0,7)+ +(12,28+j9,19)·(3,07+j0,003)=(74,01-j11,82)+(-8,16-j10,12)+(37,72-j28,1)= =103,55-j50,11
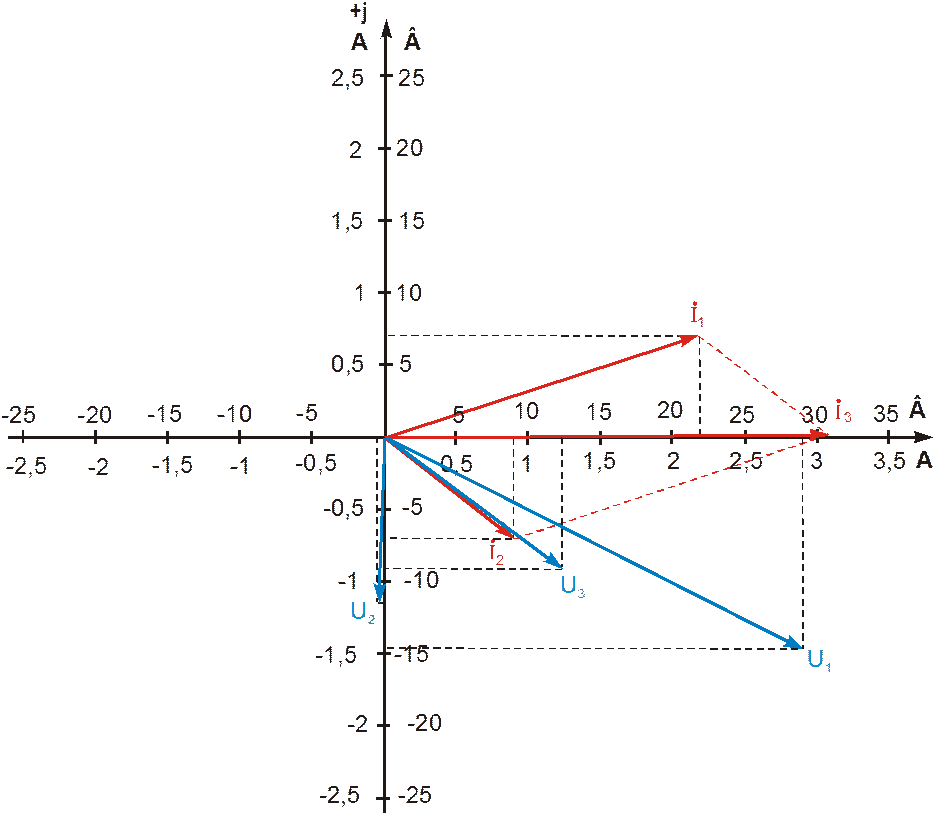Векторная
диаграмма токов и напряжений
Рисунок 3.8
3) решение задачи методом эквивалентного генератора
Преобразуем электрическую схему на рисунке 3.10 в вид более удобный для решения задачи методом эквивалентного источника и мысленно разделим схему на две части – выделенная ветвь и эквивалентный источник.
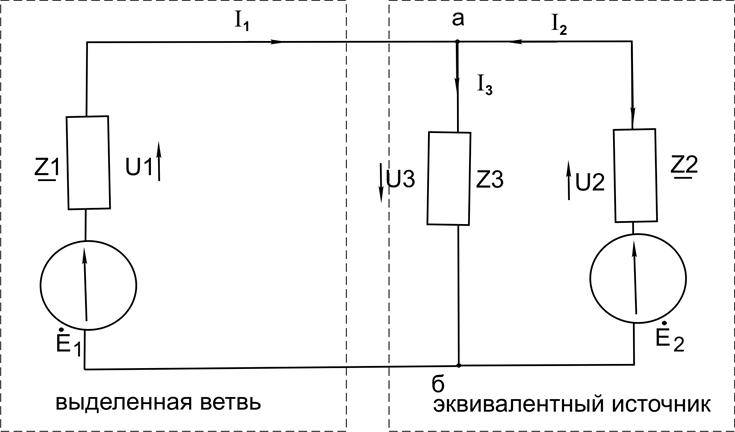
рисунок 3.10
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
