а) Определим напряжение холостого хода Uхх на выводах эквивалентного источника. Для этого воспользуемся схемой замещения той части исходной схемы замещения, которая соответствует эквивалентному источнику. Расчет схемы (рисунок 3.11) производим методом непосредственного применения законов Кирхгофа.
|
|
Составим уравнения применив первый закон Кирхгофа для одного из узлов «а» и второй закон по отношению к таким двум независимым контурам, каждый из которых включал бы в себя выводы эквивалентного источника Uхх |
рисунок 3.11
I2-I3 = 0
U3-Uxx = 0 (3.27)
U2+Uxx = E2
I2-I3 = 0
I3Z3-Uxx = 0 (3.28)
I2Z2+Uxx = E2
Из двух последних уравнений найдем токи I2 и I3:
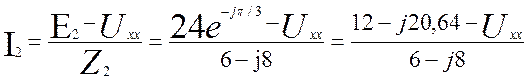(3.29)
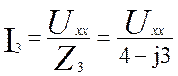(3.30)
Подставляя значения токов в первое уравнение найдем Uxx:
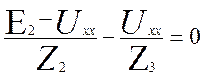(3.31)
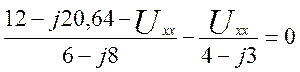
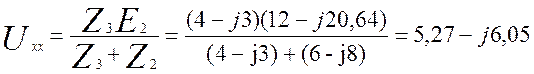
б) Рассчитаем эквивалентный источник в режиме короткого замыкания. Для этого схему замещения рисунок 3.11 представим в виде схемы выводы, в которой эквивалентного источника соединены между собой.
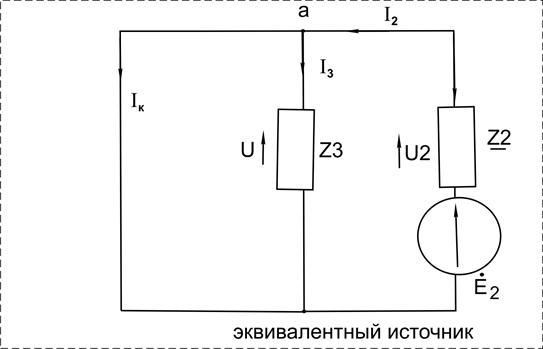
Рисунок 3.12
Из схемы изображенной на рисунке 3.12 найдем ток Iк:
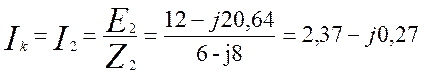(3.32)
в) по значениям Еэи и току Iк короткого замыкания, определим внутреннее сопротивление эквивалентного источника.
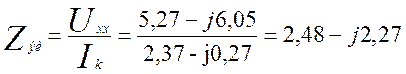(3.33)
г) представим электрическую цепь в виде простейшей схемы (одного контура) – рисунок 3.13 используя второй закон Кирхгофа, найдем ток I1:
I1 Zэи+I1 Z1 =-Eэи +E1
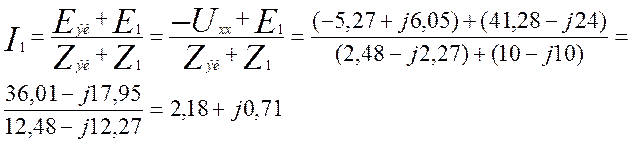(3.34)
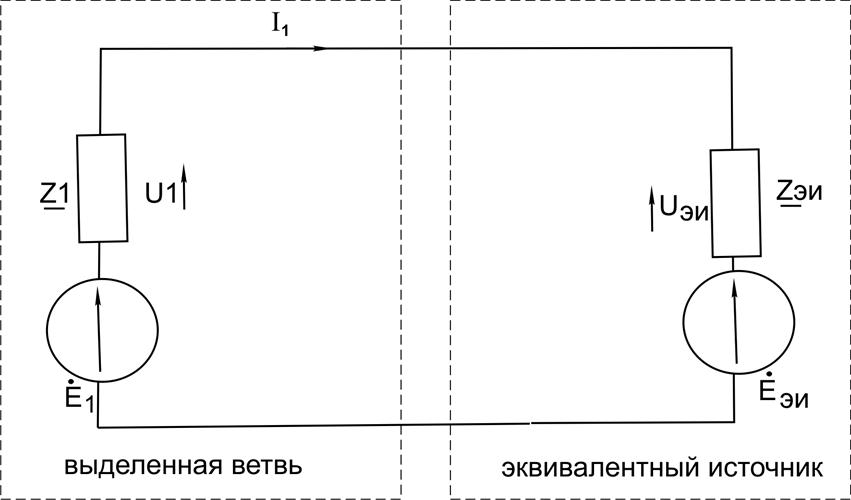
Рисунок 3.13
Как видно рассчитанные значения тока I1 с учетом погрешностей округления совпадают со значением I1 (3.5)
4 Трехфазные цепи в установившемся режиме
Задача 4
К трехфазному симметричному источнику присоединены два приемника один из которых соединен звездой, другой - треугольником. Определите токи, обозначенные на схеме (рисунок 4.1), и мощности приемников, Постройте векторные диаграммы токов и фазных напряжений. Исходные данные для решения задачи указаны в таблице 4.1.
 |
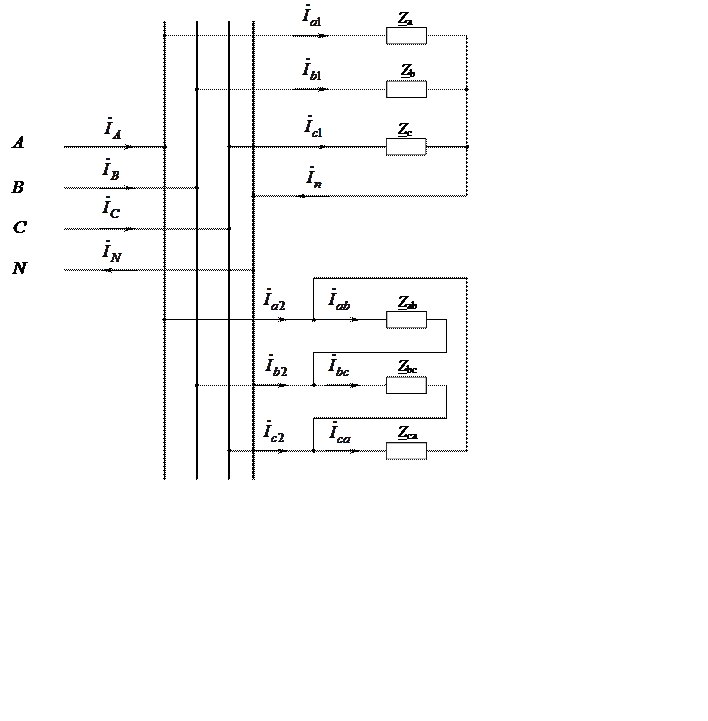Рисунок 4.1
Таблица 4.1
|
UA |
UAB |
Za |
Zв |
Zc |
Zaв |
Zвс |
Zcа |
|
220e-jπ/3 |
4-j3 |
3-j4 |
6+j6 |
4-j3 |
3-j4 |
6+j6 |
Решение задачи.
Задачу будем решать в следующем порядке: сначала определим токи, и мощности приемника, элементы которого соединены звездой и затем, определим токи и мощности приемника элементы которого соединены треугольником.
Решение задачи определения токов и мощности приемника, соединенного «звезда-звезда с нейтральным проводом»
Изобразим электрическую цепь, схема соединения которой «звезда-звезда с нейтральным проводом» рисунок 4.2
 |
Рисунок 4.2
Для определения токов составим уравнения по законам Кирхгофа, одно уравнение по первому закону относительно узла n, и три уравнения относительно контуров, показанных пунктиром:
Ia1+IB1+Ic1-IN=0
-UA+Ia1Za=0 (4.1)
-UB+IB1ZB=0
-UC+IC1ZC=0
Определим начальные фазные напряжения. Принимаем по условию симметричности:
UA=UФ=220e-j60=110-j190,5 B (4.2)
UB=220e-j180=-220 B (4.3)
UC=220ej60=110+j190,5 B (4.4)
Теперь найдем искомые токи, используя для этого системы уравнения (4.1). Предварительно переведём комплексные сопротивления из алгебраической формы в показательную:
Za=4-j3=5e-j37 (4.5)
ZB=3-j4=5e-j53 (4.6)
Zc=6+j6=8,48ej45 (4.7)
Найдем токи İа, İв, İс, İN:
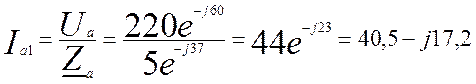А (4.8)
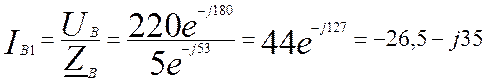А (4.9)
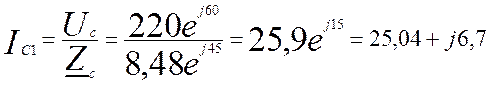А (4.10)
IN = Ia1+IB1+Ic1 = (40,5-j17,2)+(-26,5-j35)+(25,04+j6,7)=39,04-j45,5 А (4.11)
Построение векторной диаграммы (рисунок 4.3) начинаем с изображения осей комплексной плоскости и нанесения шкалы значений величин тока и напряжения, после чего в соответствующем масштабе изображаем векторы тока и напряжения.
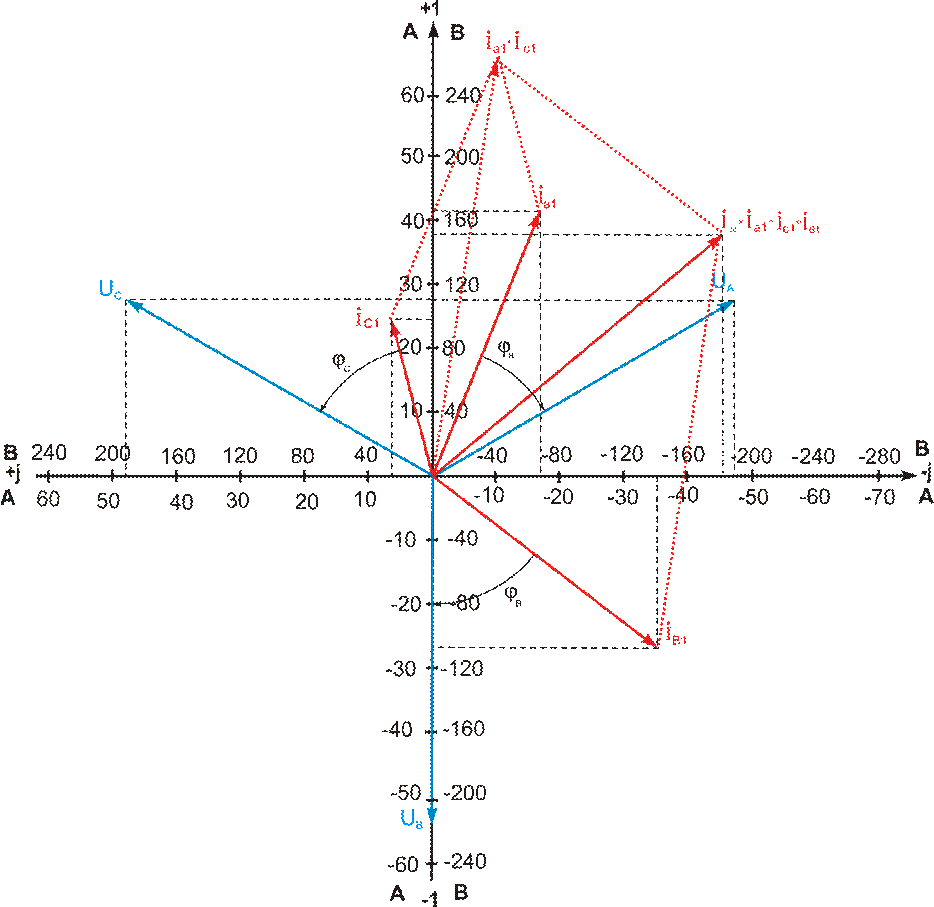
Рисунок 4.3
Анализ диаграммы позволяет установить, что фаза C в этой цепи имеет индуктивную реакцию (ток отстает по фазе относительно соответствующего фазного напряжения), фазы А и В, напротив, имеют ток, опережающий фазное напряжение, это означает, что она имеет емкостную реакцию. Ток в нейтральном проводе, как это следует из построения, показанного пунктиром красного цвета, в этой цепи не равен нулю.
Значения полной комплексной мощности определяется произведением комплексного напряжения на сопряжённый комплексный ток этого элемента:
S=U*I
Sa=Ua*Ia1=(110-j190,5)(40,5-j17,2)=1178,4-j9607,25 (4.12)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
