Линейные цепи постоянного тока в установившемся режиме. Линейные цепи переменного тока в установившемся режиме. Трехфазные цепи в установившемся режиме. Расчет линейных цепей в переходном режиме, страница 2

I R₁₂ + IR₃₅₄ – U = 0                                                                               (1.21)

I (R₁₂ + R₃₅₄) = U                                                                                   (1.22)

I = 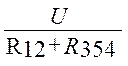= 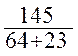  =1,66 A                                                         (1.23)

5. Определим напряжения  U12 и U354:

U₁₂ = I×R₁₂ = 1,66×64 = 106,24 B                                                           (1.24)

U₃₅₄ = I×R₃₅₄ = 1,66×23 = 38,18 B                                                          (1.25)

6. Расчет по схеме замещения рисунок (1.5) закончен, переходим к анализу схемы изображенной на рисунке (1.4):

Найдем токи I₃ и I₄:

I₃ = 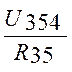==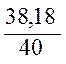0,9545 A                                                                 (1.26)

I₄ = 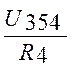==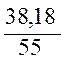0,6941 A                                                                 (1.27)

7. Определяем напряжения на резисторах:

U₁ = I×R₁ = 1,66×22 = 36,52 B                                                               (1.28)

U₂ = I×R₂ = 1,66×42 = 69,72 B                                                               (1.29)

U₃ = I₃×R₃ = 0,9545×14 = 13,36 B                                                          (1.30)

U₅ = I₃×R₅ = 0,9545×26 = 24,81 B                                                          (1.31)

U₄ = I₄×R₄ = 0,6941×55 = 38,17 B                                                          (1.32)

8. Проверим правильность решения путем составления баланса мощностей:

UI =Р = 145·1,66 = 240,7 Вт                                                                (1.33)

Р = I²R₁ + I²R₂ + I₃²R₃ + I₃²R₅ + I₄²R₄ =I²(R₁+R₂) + I₃²(R₃+R₅) + I₄²R₄ = 1,66²×(22 +42) + 0,9545²× (14 +26) + 0,6941² ×55 = 176,358 + 36,442 + 26,497 =

= 239,29 Вт                                                                                          

2) Решение методом структурных преобразований при условии,

что U= 0

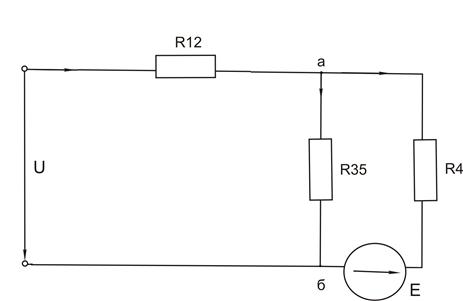
рисунок 1.6

1. При условии, что U=0 схема примет вид рисунок (1.6), определим параметры данной схемы:

R₁₂ = R₁ + R₂ = 22 + 42 = 64 Ом                                                          (1.35)

R₃₅ = R₃ + R₅ = 14 + 26 = 40 Ом                                                          (1.36)

2. Заменим две параллельно соединенные ветви R12 и R35 – одной эквивалентной ветвью образованной резистором R1235 рисунок (1.7)

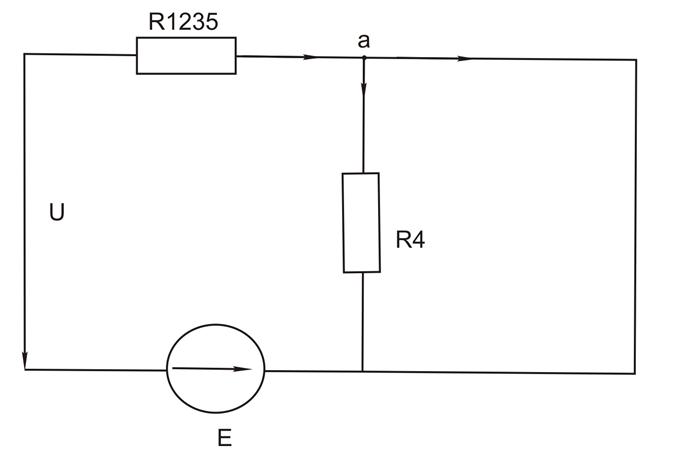
рисунок 1.7

Сопротивление этой ветви равно:

R₁₂₃₅ = 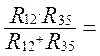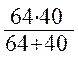=24,6 Ом                                                          (1.37)

На рисунке (1.7) представлена схема замещения состоящая из одного контура. Запишем уравнение электрического состояния цепи, используя для этого второй закон Кирхгофа. Найдем ток I₄:

I₄ = 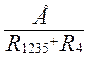= 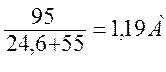                                                                 (1.38)

4. Определим напряжения U4 и U1235

U₄ = I₄×R₄ = 1,19 × 55 = 65,45 B                                                            (1.39)

U₁₂₃₅ = I₄×R₁₂₃₅ = 1,19×24,6 = 29,27 Ом                                                (1.40)

5. Теперь определим токи в цепи изображенной на рисунке (1.6)

I = 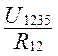= 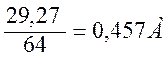                                                                      (1.41)

I₃ = 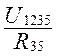= 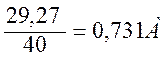                                                                     (1.42)

6. Вычисляем напряжение на резисторах R1, R2 и R3R5

U₁ = I₁×R₁ = 0,457 × 22 = 10,05 B                                                         (1.43)

U₂ = I₁×R₂ = 0,457 × 42 = 19,19 B                                                          (1.44)

U₃ = I₃×R₃ = 0,731 × 14 = 10,23 B                                                          (1.45)

U₅ = I₃×R₅ = 0,731 × 26 = 19 B                                                               (1.46)

7. Для проверки правильности решения задачи составим баланс мощностей:

EI₄ = 95 · 1,19 = 113,05 Вт                                                                  (1.47)

I₁²(R₁ + R₂) + I₃²(R₃ + R₅) + I₄²·R₄= 0,457²·64 + 0,731² 40 + 1,19²·55 = 13,36 + 21,374 + 77,885 = 112,61 Вт                                                                       (1.48)

Сравнивая результаты с учетом погрешностей округления, делаем вывод – задача решена правильно. Баланс мощностей имеет место быть.

3) Решение задачи методом наложения.

Принцип решения: исходная цепь представляет собой совокупность частных схем замещения, обозначения токов и напряжений индексируются – первый, обозначает ток и напряжение в исходной схеме, второй – номер источника, присутствующего в схеме.

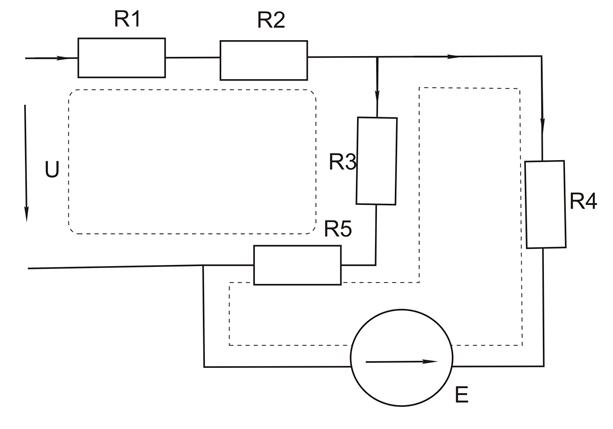
рисунок 1.8

Исходная схема приведена на рисунке 1.8. Расчет частных схем производится методом структурных преобразований. Мысленно удалим ЭДС из схемы и оставим один источник. Из этого схема будет соответствовать схеме на рисунке 1.9.

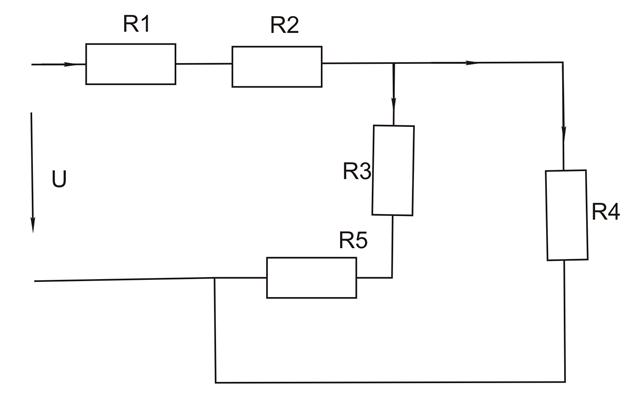
рисунок 1.9

Для этой схемы мы уже определяли параметры:

I_1.1 = 1,66 A                                                                                  (из 1.23)

I_3.1 = 0,9545 A                                                                              (из 1.26)

I_4.1 = 0,6941 A                                                                              (из 1.27)

Найдем параметры для второй частной схемы, изображенной на рисунке 1.10

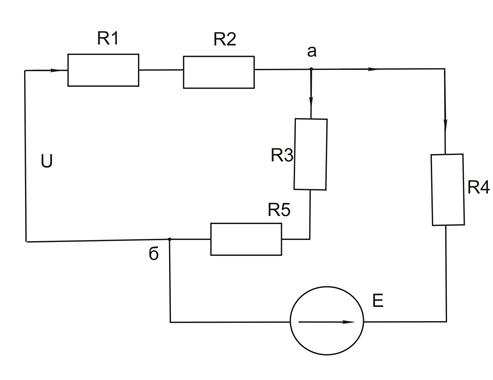
рисунок 1.10

Для этой схемы мы так же определяли параметры:

I_1.2 = 0,457 A                                                                                (из 1.41)

I_3.2 = 0,731 A                                                                                (из 1.42)

I_4.2= 1,19 A                                                                                  (из 1.38)

Теперь просуммируем частные токи с учетом направления в схемах.

I = I_1.1 - I_1.2 = 1,66 - 0,457=1,203 A                                                       (1.49)