Линейные цепи постоянного тока в установившемся режиме. Линейные цепи переменного тока в установившемся режиме. Трехфазные цепи в установившемся режиме. Расчет линейных цепей в переходном режиме, страница 7

Sb=U_B*I_B1=-220(-26,5-j35)=5830+j7700                                                           (4.13)

Sc=U_c*I_c1=(110+j190,5)(25,04+j6,7)=1478,05+j5507,12                                 (4.14)

Решение задачи определения токов и мощности приемника, соединенного «треугольником».

Рисунок 4.4

Электрическая схема изображенная на рисунке 4.4 имеет три узла (а, в, c) и три независимых контура на схеме обозначенные пунктирной линией. Составим систему уравнений по первому закону Кирхгофа, для узлов (а, в, c) и три уравнения применяя второй закон Кирхгофа для независимых контуров:

                                                                

                                                                

                                                                                     (4.15)

                                                                

                                                                

Из условий задачи ψ_а=-π/3=-60⁰, а из формул (4.3) и (4.4) имеем:

ψ_в=-π=-180⁰

ψ_с=π/3=60⁰

Найдём:

ψ_ав= ψ_а +π/6==-π/3+π/6=-π/6=-30⁰

ψ_вc= ψ_аb -2π/3==-π/6-2π/3=-5π/6=-150⁰

ψ_ca= ψ_аb+2π/3==-π/6+2π/3=π/2=90⁰

По условию симметричности определим начальные фазы напряжений U_АВ; U_ВС; U_СА:

U_AВ= 220e ^-j30 =190,5-j110 B                                                                  (4.16)

U_BС=220e^-j150=-190,5-j110 B                                                                  (4.17)

U_CА=220e^j90=j220 B                                                                                (4.18)

Значения фазных напряжений токов найдены, найдем линейные токи из трех последних уравнений системы 4.15.

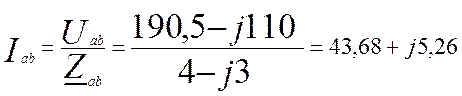 А                             (4.19)

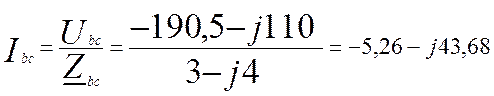 А                         (4.20)

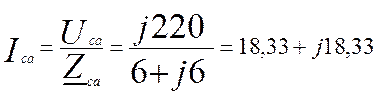 А                                         (4.21)

Из первых трех уравнений системы (4.15) найдем линейные токи I_А2; I_В2; I_С2

 А,                (4.22)

 А       (4.23)

 А       (4.24)

Для построения векторной диаграммы задаемся масштабом напряжения и тока, после чего результаты расчета представляем в векторной форме. Векторная диаграмма приведена на рисунке 4.5

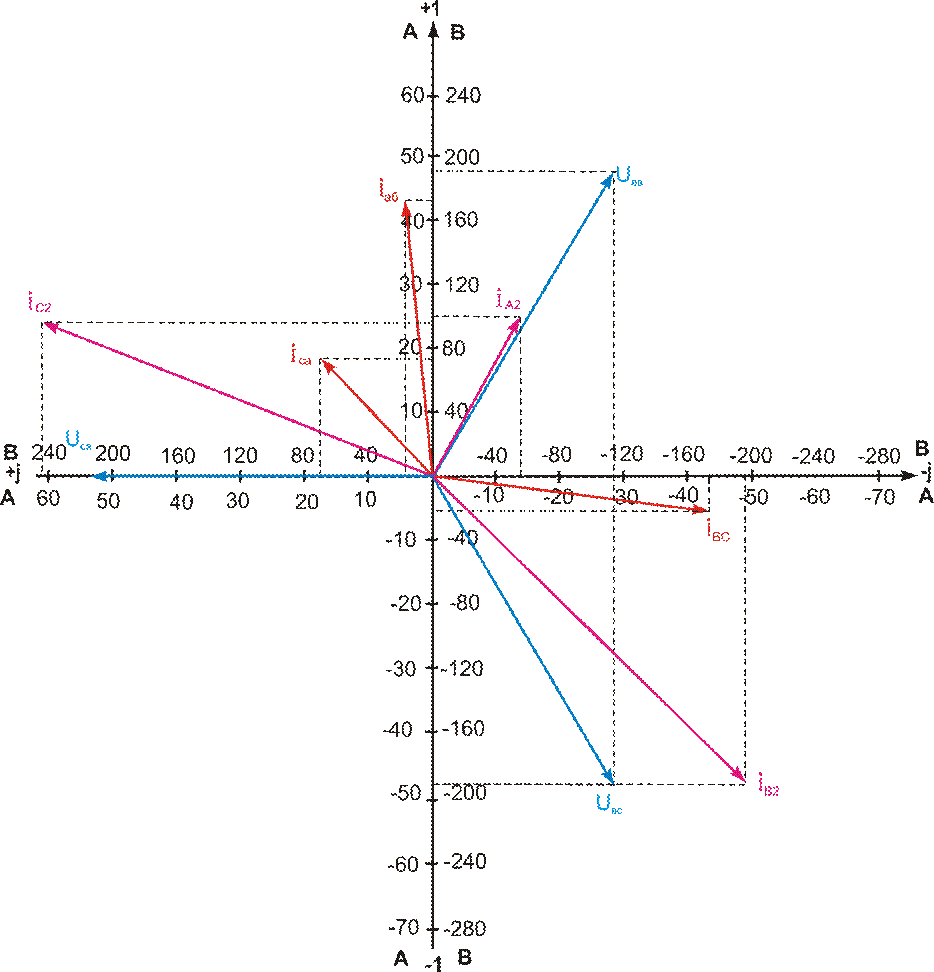
Рисунок 4.5

Значения полной комплексной мощности S элемента определяется как произведение комплексного напряжения на сопряженный комплексный ток этого элемента:

S_ab=U_abI_ab=(190,5-j110)(43,68+j5,26)=8899,64-j3802,77                                 (4.25)

S_bc=U_bcI_bc=(-190,5-j110)(-5,26-j43,68)=-3802,77+j8899,64                             (4.26)

S_ca=U_caI_ca=j220(18,33+j18,33)=-4032,6+j4032,6                                               (4.27)

5. Расчет линейных цепей в переходном режиме

Задача 5

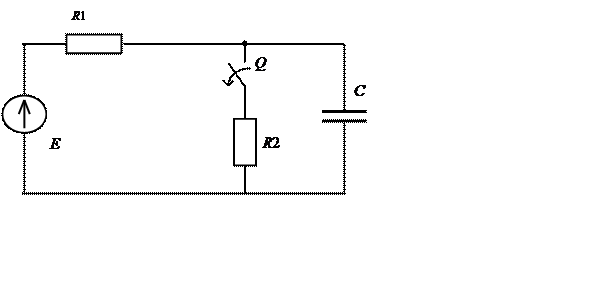Определите токи в ветвях и напряжения на элементах цепи до и после коммутации. Постройте графики изменения этих величин во времени. Схема цепи представлена на рисунке 5.1. Параметры элементов цепи указаны в таблице 5.1

Рисунок 5.1

Таблица 5.1

Е	R1	R2	L	C
100	3 Ом	50 Ом	-	50

1. Схема замещения до коммутации имеет вид, рисунок 5.2.

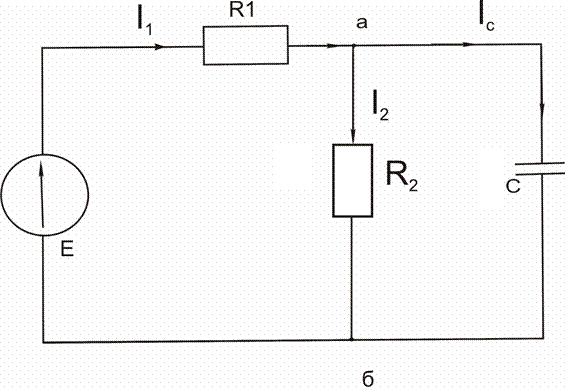
Рисунок 5.2

В соответствии с первым законом Кирхгофа запишем уравнение:

I₁-I₂-I_c=0                                                                                       (5.1)

Ток на конденсаторе до коммутации I_c=0, тогда уравнение (5.1) примет вид:

I₁=I₂

Найдём ток I₁:

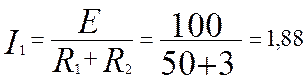 A                                                                           (5.2)

Найдём напряжение U_c до коммутации:

U_c=U_R2=I₂R₂=1,88*50=94 B                                                       (5.3)

2. Схема замещения после коммутации имеет вид, рисунок 5.3.

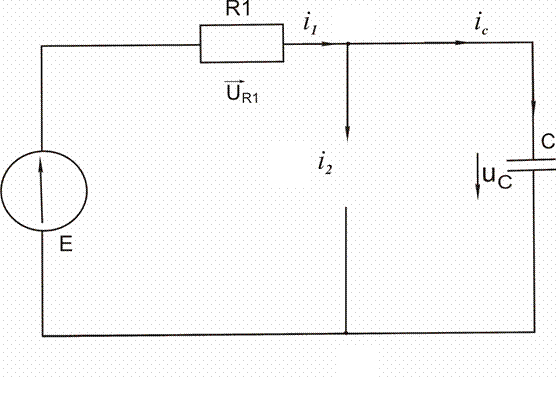
рисунок 5.3.

Запишем систему уравнений:

i₁- ic-i₂=0                                                                       (5.4)

U_R1+U_c=E

Из схемы замещения видно, что i₂=0. Значит первое уравнение из системы (5.4) примет вид:

i₁=ic

Используя модель идеального конденсатора, запишем зависимость:

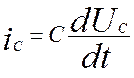                                                                                            (5.5)

Найдём U_C:

U_C=U_Cпр+ U_Cсв                                                                                       (5.6)

U_Cсв= Аe^pt                                                                                              (5.7)

Корень характеристического уравнения р равен:

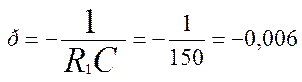                                                                    (5.8)

U_Cсв= Аe^-0,006t                                                                                         (5.9)

Подставим значения U_C и U_Cсв в уравнение (5.6) и найдём постоянную интегрирования А при t=0:

U_C=U_Cпр+ U_Cсв

94=100+Ae^-0,006t

A=-6

Уравнение (5.6) в послекоммутационном режиме примет вид:

U_C=100-6е^-0,006t

Подставим значение U_C в уравнение (5.5) для расчёта i_C:

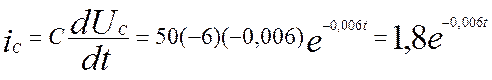                              (5.10)

На основании полученных вычислений построим графики i_cи U_с рисунок 5.4 и 5.5:

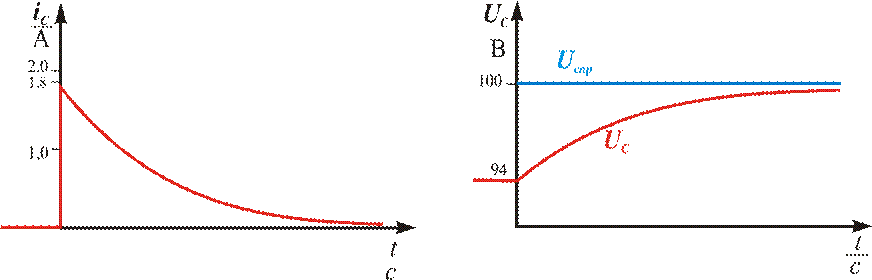
Рисунок 5.4                                                   Рисунок 5.5

Литература:

1.  «Электротехника и электроника: Общая электротехника и электроника: Методические указания и контрольные задания для студентов заочной формы обучения» / Автор-сост. М.Г. Колонутов; НовГУ им. Ярослава Мудрого. – Великий Новгород, 2006.

2.  «Задачник по теории линейных электрических цепей» Автор-сост.

Шебес Н.Р., Каблукова М.В. 1990г.

3.  Конспект лекций «Общая электротехника и электроника»

4.  При расчётах использован «Простейший калькулятор комплексных чисел CNC v 1.0». Сайт: http://www.freeware.ru/program_prog_id_9395.html

5.  «Комплексные числа. Линейная и векторная алгебра».

Автор: Мозалёва Е.М.