БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ
КАФЕДРА ОБЩЕЙ ФИЗИКИ И ЭЛЕКТРОТЕХНИКИ
Общая электротехника
Вариант 42.
“_____” ___________2005
2005
Задача №1 (Переходные процессы).
Дана электрическая цепь:

|
E, В |
L, мГн |
C, мкФ |
R1 |
R2 |
R3 |
R4 |
Определить |
|
150 |
2 |
5 |
4 |
10 |
5 |
6 |
I3 |
1. Классический метод.
1) Схема до коммутации:
|

Очевидно, что iL(0-)=0; Uc(0-)=E=150 В.
По законам коммутации: iL(0+)=0; Uc(0+)=150 В.
2) Принужденные значения (после коммутации):
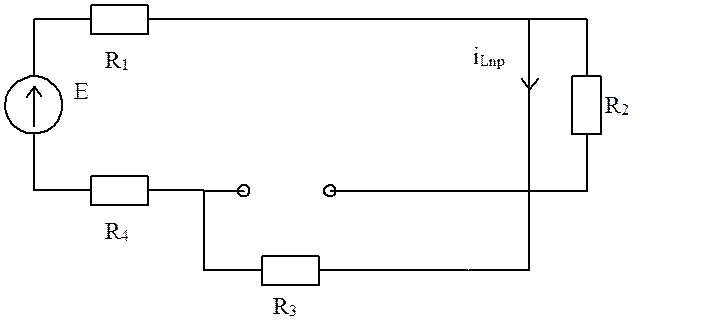 Rобщ=R1+R3+R4=15
(Ом)
Rобщ=R1+R3+R4=15
(Ом)
ILпр=E/Rобщ=10 (А)
Uc пр= ILпрR3=50 (В)
![]()
|
 |
3) Свободные составляющие:
ILсв(0)= iL(0+)- ILпр=-10 А; Uc св(0)= Uc(0+)- Uc пр=100 В
4) Составляем характеристическое уравнение (ХУ) по входному сопротивлению схемы (Zвх=0):
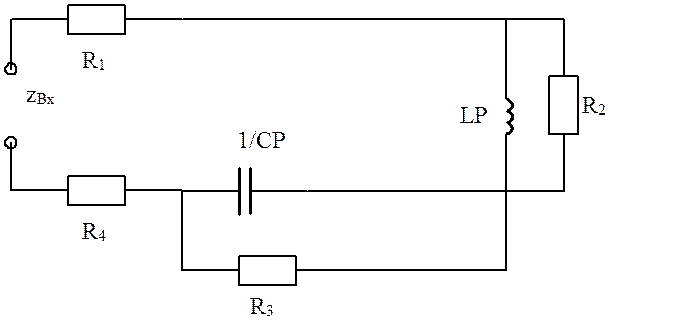 Zвх=
Zвх=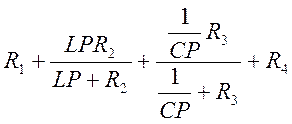 =
=
=10+ 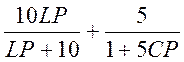 =100LCP2+
=100LCP2+
+25LP+500CP+150=
=10-6P2+0.053P+150=0
D=0.0532-4*10-6*150=2.156*10-3
p1=(-0.053+0.046)/2*10-6=-3032; p2=(-0.053-0.046)/2*10-6=-49468
5) Решение для свободной составляющей:
I3св(t)= A1ep(1)t+A2ep(2)t=A1e-3032t+A2e-49468t, определим А1 и А2.
6) Составим систему уравнений
i3 св(t)=A1ep(1)t+A2ep(2)t и di3 св(t)/dt=A1p(1)ep(1)t+A2p(2)ep(2)t
i3 св(0)=A1+A2; di3 св(0)/dt=A1p1+A2p2 (*)
7) Составим систему уравнений по законам Кирхгофа
![]()
![]()
|
|
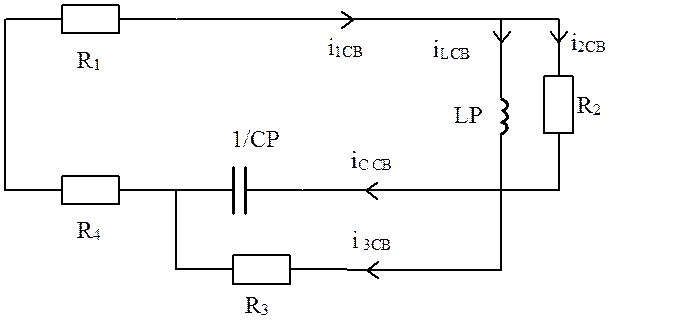
Возьмем производные от этих уравнений
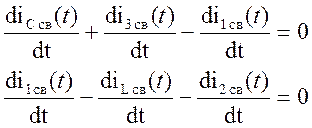

|
1 ЗК:
IC св(0)+i3 св(0)-i1 св(0)=0 (1)

 i1 св(0)-iL св(0)-i2
св(0)=0 (2)
i1 св(0)-iL св(0)-i2
св(0)=0 (2)
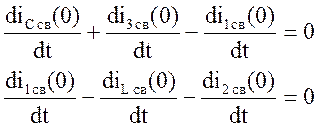
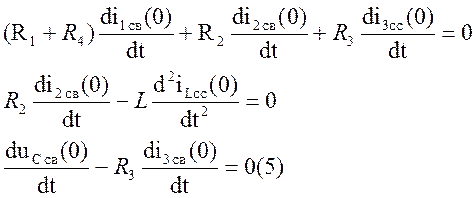
Систему можно добавить уравнением:
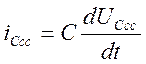 ;
;
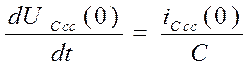
Из (4): i3 св(0)= uС св(0)/R3=20 (A)
Из (5): 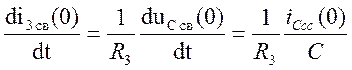
Из (1): IC св(0)= i1 св(0)- i3 св(0)
Из (2): i2 св(0)= i1 св(0)-iL св(0)= i1 св(0)+10
Из (3): I1 св(0)(R4+ R1)+ [i1 св(0)+10]R2+ i3 св(0)R3=0 или
10 i1(0)+10 i1(0)+100+20*5=0; i1св(0)=-10 (A)
IC св(0)=
-10-20=-30(A) 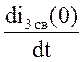 =
-1.2*106
=
-1.2*106
8) Вернемся к системе (*):
20=A1+A2
-1.2*106= -3032A1-49468A2
A1= -4.536
A2=24.536
9) i3 св(t)= -4.536e-3032t+24.536 e-49468t
i3(t)= i3 св(t)+ i3 пр(t)=10 – 4.536 e-3032t + 24.536 e-49468t (A)
2. Операторный метод.
1) Найдем ток индукции и напряжение на емкости в цепи до коммутации (см. классический метод):
iL(0-)=0; Uc(0-)=E=150 В.
2) Составим схему замещения после (после коммутации).
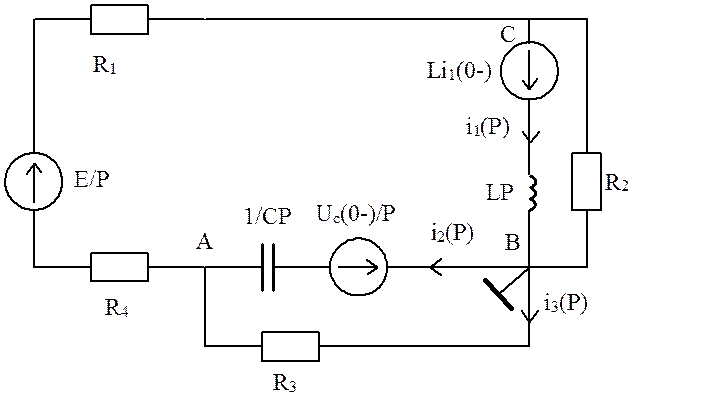
Найдем i3(P) МУП.
φB=0.
Для узла А: φA(gC+g3+g14)- φcg14= -(Uc0-/P)gC-(E/P)g14
Для узла C: φc(g14+ g1+g2)- φAg14=(E/P)g14-Li10- (1)
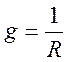 , отсюда: g1=
, отсюда: g1=![]() ,
g2=0.1, g3=0.2, g14=0.1, gc=CP.
,
g2=0.1, g3=0.2, g14=0.1, gc=CP.
Подставляя эти значения в систему (1), получим:
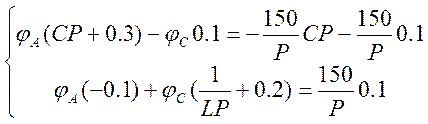
Решим ее через определитель:
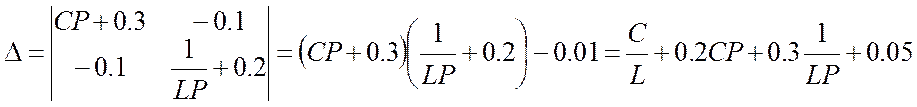
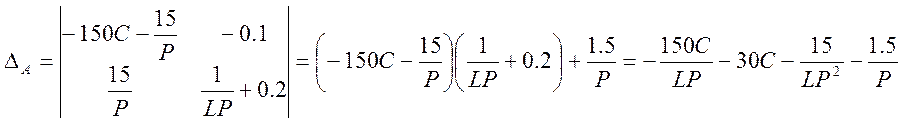
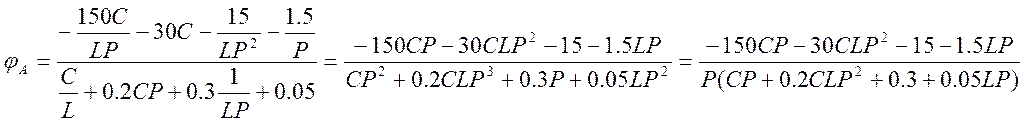
3) Переходим к оригиналу φA.
N(P)= ![]() = -3*10-7 P2-3.75*10-3 P-15
= -3*10-7 P2-3.75*10-3 P-15
M(P)= ![]() =P(2*10-9
P2+1.05*10-4 P+0.3)
=P(2*10-9
P2+1.05*10-4 P+0.3)
Найдем корни характеристического уравнения
P0=0; 2*10-9 P2+1.05*10-4 P+0.3=0;
D=8.625*10-9
P1= -3032
P2= -49468
Решение φA при трех корнях:
φA(t)=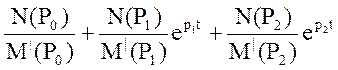
M/(P)= 3*2*10-9 P2+2*1.05*10-4P+0.3
N(P0)=-15 M/(P0)= 0.3
N(P1)= -6.3874 M/(P1)= -0.282
N(P2)= -563.61 M/(p2)= 4.594
φA(t)= -50 +22.6816 e-3032t - 122.68 e-49468t
По закону Ома для участка цепи: 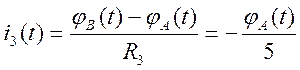 (φB=0, R3=5 Ом), получаем:
(φB=0, R3=5 Ом), получаем:
i3(t)= 10 – 4.536 e-3032t + 24.536 e-49468t (A)
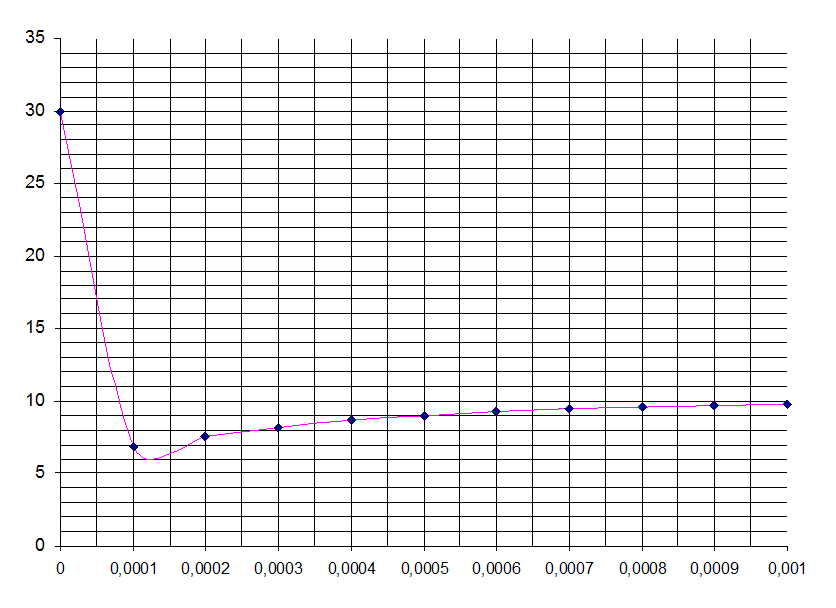
3. Построим график i3(t).
Конечное значение времени: 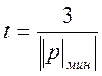 , |p|мин=-3032
– меньший по модулю корень ХУ
, |p|мин=-3032
– меньший по модулю корень ХУ
Интервал времени: [ 0, 10-3 ]c
|
t |
0 |
0,0001 |
0,0002 |
0,0003 |
0,0004 |
0,0005 |
0,0006 |
0,0007 |
0,0008 |
0,0009 |
0,001 |
|
i3(t) |
30 |
6,8247 |
7,5277 |
8,1734 |
8,6512 |
9,0039 |
9,2645 |
9,4568 |
9,5989 |
9,7038 |
9,7813 |
|
|
Задача №2 (Интеграл Дюамеля).
Дана электрическая схема:
![]()
![]()
![]()
![]()
![]() i1 R
i1 R
![]()
![]()
![]()
![]() Определить UR
Определить UR

![]() UR i2
i3
UR i2
i3
U1 C R
U1 – напряжение на входе, изменяющееся со временем по заданному закону U1(t):
![]() U1
U1
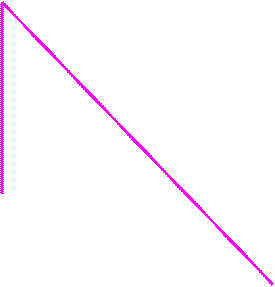 |
UBX1=A-kt
A
t1 UBX2=0
![]()
![]()
![]() t
t
0
A/2
![]()
![]() Подадим на вход испытательную функцию Хевисайда 1(t) =
1/p. Рассчитывать искомую величину будем операторным
методом при нулевых начальных условиях (внутреннее ЭДС конденсатора равно нулю)
Подадим на вход испытательную функцию Хевисайда 1(t) =
1/p. Рассчитывать искомую величину будем операторным
методом при нулевых начальных условиях (внутреннее ЭДС конденсатора равно нулю)
I1(P) R
 |
|||

![]()

![]() 1
1
1
1
p Cp R
![]()
UR(P)=i(P)R=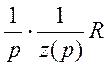 ;
;
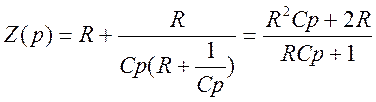
UR(P)=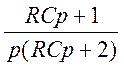 ;
;
M(P)=p(RCp+2)=0; N(P)=RCP+1
p0=0;
p1=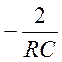 ; M΄(P)=2RCP+2
; M΄(P)=2RCP+2
N(P0)=1; M΄(P0)=2;
N(P1)=-1; M΄(P1)=-2;
Перейдем к оригиналу: UR(t)=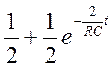 =h(t) – переходная функция по напряжению.
=h(t) – переходная функция по напряжению.
Запишем интеграл Дюамеля для участка от 0 до t1 (функция показывает напряжение в момент t):
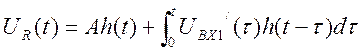 UBX1(t)=U1=A-kt– из графика UBX1΄(t)=-k= UBX1΄(τ)
UBX1(t)=U1=A-kt– из графика UBX1΄(t)=-k= UBX1΄(τ)
h(t-τ)= 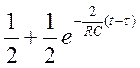
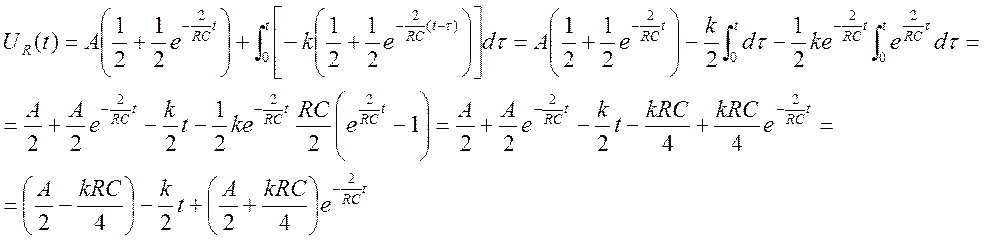
Запишем интеграл Дюамеля для участка от t1 до ∞
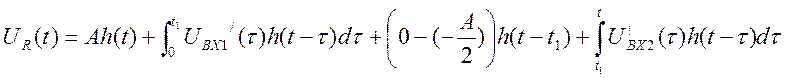
h(t-t1)=
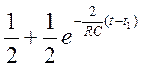
UBX2 (t)=0;
UBX2΄(t)=0; 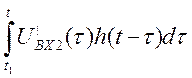 =0
=0
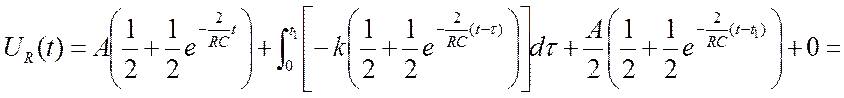
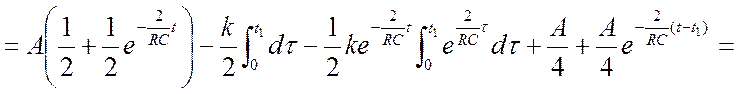
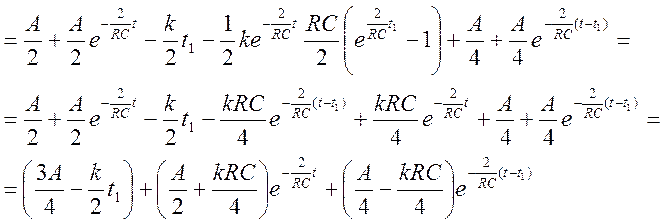
Задача №4 (Спектральный метод).
Получить спектр функции |U(jω)|
Заданы аналитическое выражение и график для импульса.
![]() U(t)=U0e-αt
U(t)=U0e-αt
α=50 (1/c); U0=150 В
1. Получение аналитического выражения для модуля и аргумента спектра функции.
По таблице 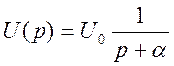 Заменим p на jω:
Заменим p на jω:
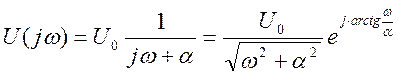
2. Представим ![]() как функцию безразмерной величины
ω/α
как функцию безразмерной величины
ω/α
![]() =
=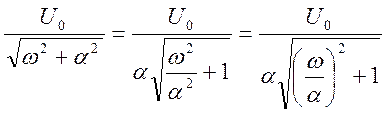 ;
;
3.Построим график ![]() =
=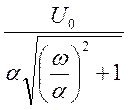 =
=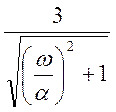 в
функции от ω/α
в
функции от ω/α
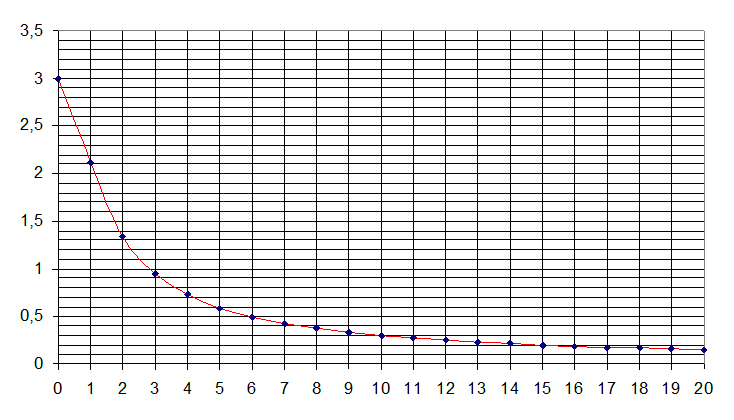
![]()
ω/α
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.