БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ
КАФЕДРА ОБЩЕЙ ФИЗИКИ И ЭЛЕКТРОТЕХНИКИ
Расчетно-графическая работа №5
по дисциплине
общая электротехника
Синтез электрических цепей, дискретные цепи.
Вариант №42, №23.
Выполнил ст. гр. УИТ-22
Принял преподаватель
“_____” ___________2005г
2005г.
Задание №1 (Синтез электрических цепей). В-42.
Значения полиномов числителя и знаменателя входного сопротивления z(p) двухполюсника:
|
a4 |
a3 |
a2 |
a1 |
a0 |
b4 |
b2 |
b |
|
6 |
2 |
10 |
3 |
1 |
6 |
10 |
1 |
1)
Z(p)=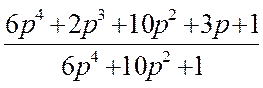 =
=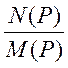
2) Реализуем данный двухполюсник лесничной схемой. Разделим многочлен на многочлен по порядку синтеза:
6p4+2p3+10p2+3p+1 |6p4+10p2+1
6p4+ 10p2+ 1 | 1 (z1)
6p4+10p2+1| 2p3+ 3p
6p4+ 9p2 | 3p (y2)
2p3+3p | p2+1
2p3+2p | 2p (z3)
p2+1| p
p2 | p (y4)
p | 1
p | p (z5)
0
Получим схему:
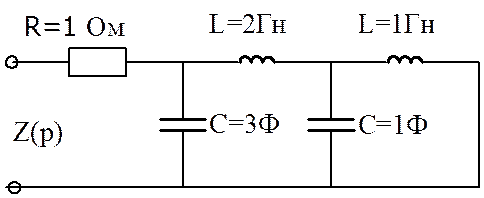
Задание №2 (дискретные цепи). В-23
Заданы входная последовательность: x(t)=sin(0,5n)u(n), дискретное время Td=0,05 c,
передаточная функция: w(p)=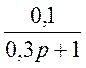
1)Проведем z-преобразование входной последовательности по таблице:
x(z-1)=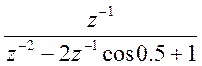
2)Перейдем от передаточной
функции аналогового четырехполюсника к передаточной функции соответствующего w(z).
Для этого заменим p на 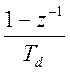 :
:
w(z)= 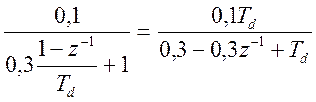 , при Td=0,05 c:
, при Td=0,05 c:
w(z)=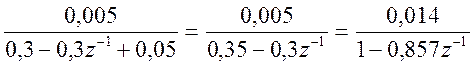
3)Реализуем передаточную функцию цифрового 4-хполюсникав виде схемы:
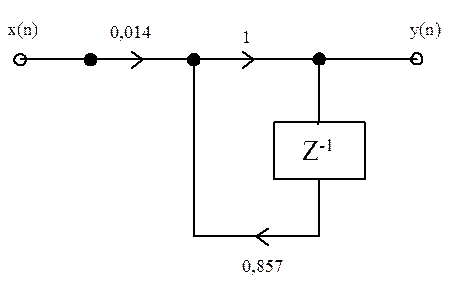
4)Найдем z-преобразования выходной последовательности Y(z)=W(z)X(z):
y(z-1)=
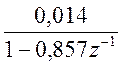
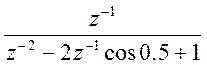 =
=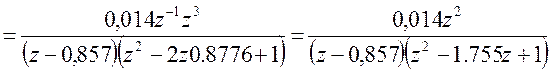
y(z)= 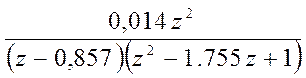 =
=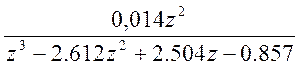
5)Запишем выражение для выходной последовательности y(nT), для этого используем обратные z-преобразования.
y(n)=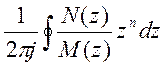
Корни полинома знаменателя: z1=0.857
D=-0.92;
z2,3=0.877![]() 0.48i
0.48i
y(n)=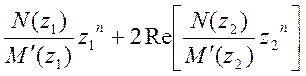 (1)
(1)
N(z)= ![]()
M(z)= ![]()
![]()
Подставляя в (1) найденные значения, получаем:
N(z1)= 0.0103
N(z2)= 0.0076+0.0118i
M′(z1)= 0.23
M′(z2)= -0.46+0.02i
y(n)=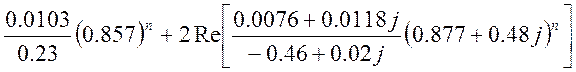 =
=
![]()
=![]() =
= ![]() 0.06 cos
0.06 cos![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.