БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ
Выполнил ст. группы УИТ-22
Калюжный А.А.
Принял:
Олькова В.Б_______________
«_____» ____________ 2001 г.
2002
Лабораторная работа №1
Переходные процессы
Для данной лабораторной работы были взяты следующие начальные данные: L=0.1 Гн, U=10 B, R1=Rзаряд=2*103 Ом, R2=Rразр=748 Ом.
![]()
![]() RЗАРЯД К1
RЗАРЯД К1
 |
 |
||||
 Реле L
Реле L

![]()
![]()
![]()
![]() 1 2
1 2
![]()
![]()
![]()
![]()
![]()
![]() E
E
 C
C
 |
Рассмотрим процесс зарядки конденсатора. Ключ К1 замкнут, и реле находится в положении -1
UC СВ(0_)=0
IПРR1+UC ПР=E, но IПР=0 то UC ПР=Е или что тоже самое UC ПР=10 (В)
UC CB(0)= UC СВ(0+)- UПР=-10 (В)
Z(p)=R1+1/Cp Приравнивая Z(p)=0 получим характеристическое уравнение: R1+1/Cp=0
Решаем уравнение относительно p: p=-1/RC
При одном корне характеристического уравнения получаем решение для свободной составляющей напряжения на конденсаторе: UC CB(t)=Aept. Перепишем решение для момента времени t=0: UC CB(0)=A, но UC CB(0)=-10(В). Следовательно А=-10, отсюда получаем UC CB(t)=-10ept. Общее решение : UC (t)=UПР+UC CB(t), UC (t)=10-10e-t/RC.
Записываем решение для момента времени t=τ : UC(t)=10-10e-τ/RC=10(1- e -1)=6.32 (B)
τ=|1/p| =|1/R1C|=R1C, отсюда электроёмкость будет равна: С=τ/R1
Из изображения полученного на осциллографе определяем время τ: τ=0,002(с). Тогда С =1 мкФ. Отсюда получаем график процесса зарядки конденсатора:
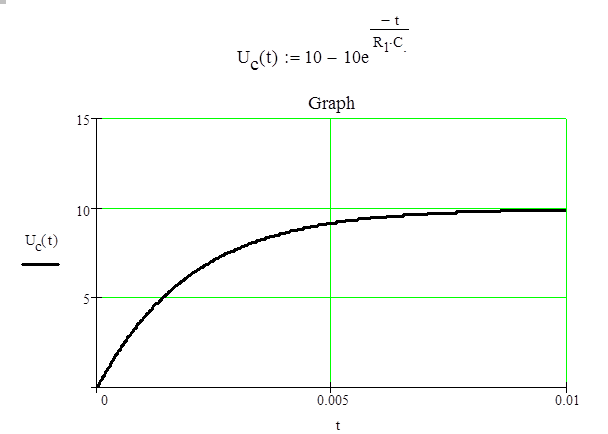
Рассмотрим процесс разрядки конденсатора на разрядное сопротивление RРАЗРЯД=R2. Задачу по нахождению UC(t) будем решать классическим методом. Определяем ток через индуктивность и напряжение на ёмкости в момент времени t=0_: i(0_)=0 , UC(0_)=10 (B). Определяем принуждённую составляющую тока через индуктивность и принуждённое напряжение на ёмкости: IПР=0, UС ПР=0, так как нет ЭДС.
Определяем свободные составляющие в момент времени t=0:
iCВ(0)=i(0+)-iПР=i(0_)-iПР=0
UC CВ(0)=U(0+)-UПР=U(0_)-UПР=10 (B)
Составляем характеристическое уравнение
Z(p)=R2+Lp+1/Cp, приравнивая Z(p)=0 или тоже самое что и
R2+Lp+1/Cp=0 и делая необходимые математические преобразования получаем квадратное уравнение, которое решается относительно –p:
p2+p*(R2/L)+1/LC=0
p1,2=-R2/2L±√( R2/2L)2-1/LC
p1=-1741, p2=-5736,9. Данные значения корней характеристического уравнения говорят о том что процесс апериодический.
Составим закон по которому изменяется свободная составляющая напряжения: UC CB(t)=A1ep1t+ A2ep2t. Для нахождения коэффициентов А1 и А2 составляем систему уравнений состоящую из решений и производных от решения до (n-1) порядка включительно (где n степень характеристического уравнения).
dUС СВ(t)/dt= A1 p1ep1t+ A2 p2ep2t, переписываем систему уравнений для момента времени t=0:
![]() UC CB(0)=A1+ A2
UC CB(0)=A1+ A2
dUС СВ(t)/dt= A1 p1+ A2 p2
Ток через ёмкость i=C (dUC /dt) или iCB(0) =C (dUC CB(0) /dt) откуда dUC CB(0) /dt= iCB(0)/C=0. Тогда получаем систему уравнений, которую решаем методом Краммера-Копели :
![]() A1+ A2=10
A1+ A2=10
A1 p1+ A2 p2=0
Высчитаем определитель матрицы проводимости g, ∆ :
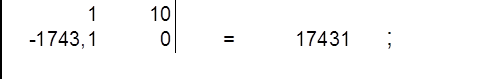
найдём определитель матрицы ∆1 :
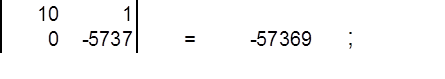
найдём определитель матрицы ∆2 :
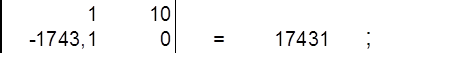
Отсюда получаем : А1 = ∆1/∆ =14,36, А2 = ∆2/∆=-4,36.
Составляем решение для напряжения на конденсаторе:
UC (t)= UПР + UC СВ(t)
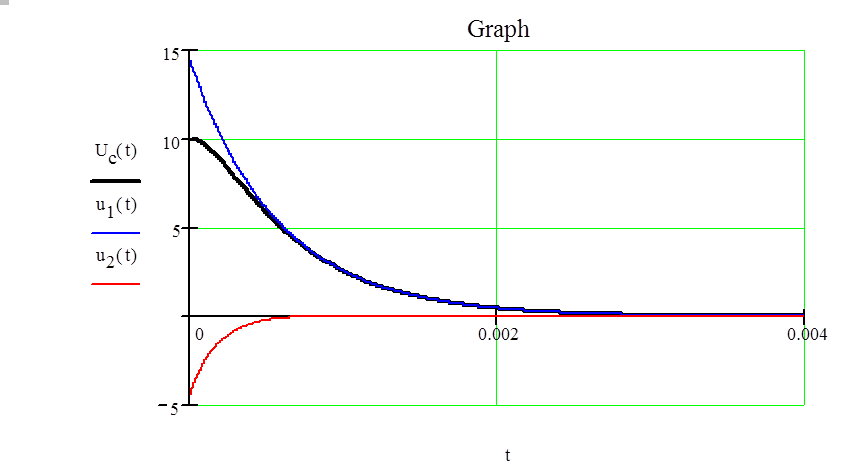
UC (t)= 14.36e-1743.1t – 4.36e-5736.9t
Построим получившуюся зависимость
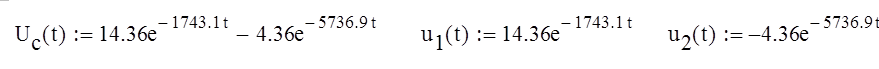
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.