Статистический анализ цен на продукты питания в РФ, страница 12

Введем обозначения: x_i  - уровень цен (цена), y_i – уровень потребления (потребление).

3. Оценка тесноты связи между признаками.

3.1. Предположим, что изучаемые признаки связаны линейной зависимостью рассчитаем линейный коэффициент корреляции по формуле:

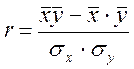_,                                                                                     (32)

где ,         (33)                                 (34)

 

101,58	58,85	6911,9	13970,53	3826,54

Таблица 9

 Данные для расчета линейного коэффициента корреляции

Вычислим r:

_.

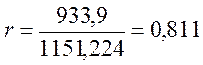Коэффициент линейной корреляции равный 0,811 свидетельствует о наличии сильной прямой связи.

3.2. Оценка существенности коэффициента корреляции. Для этого найдем расчетное значение  t-критерия Стьюдента:

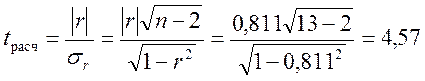.                                              (35)

По таблице критических точек распределения Стъюдента найдем t_кр при уровне значимости  и числе степеней свободы  

t_кр=1,8.

Так как , линейный коэффициент считается значимым, а связь между x и y – существенной.

4.  Построение уравнения регрессии.

Этап построения регрессионного уравнения состоит в оценке его параметров, оценке их значимости оценке значимости уравнения в целом.

4.1. Идентификация регрессии. Построим линейную однофакторную регрессионную модель вида . Для оценки неизвестных параметров a₀, a₁ используется метод наименьших квадратов, заключающийся в минимизации суммы квадратов отклонений теоретических значений зависимой переменной от наблюдаемых.

Система нормальных уравнений для нахождения параметров a₀,a₁ имеет вид:

                                                                                                (36)

Решением системы являются значения параметров:

a₀=46,55

a₁ =0,16.

Составим уравнение регрессии:

.

Коэффициент детерминации(Рисунок 4), показывает, что 91% вариации признака «Уровень потребления» обусловлено вариацией признака «Цены на мясо говядины», а остальные 9% вариации связано с воздействием неучтенных в модели факторов.

4.2.  Проверка значимости параметров регрессии.

 ,.,  t_кр=1,8. Так как в обоих случаях , то параметры   и  являются значимыми.

4.3. Проверка значимости уравнения регрессии в целом.

 , .98,7 (Рисунок 4). По таблице критических значений критерий Фишера . Так как , то уравнение регрессии можно считать значимым.

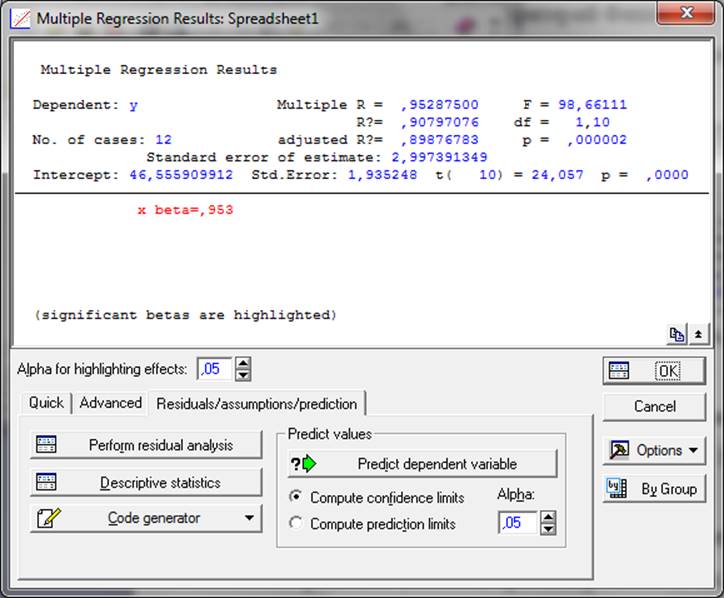
Рисунок 4 – Результаты КРА, проведенного в Statistica.

Таким образом, судя по регрессионному коэффициенту a₁ =0,16, можно утверждать, что при изменение цены на 1 единицу уровень потребления в среднем изменится на 0,16 кг в год.

5. Использование регрессионной модели для принятия управленческих решений (анализа, прогнозирования и т.д.)

Вычислим прогнозное значение уровня потребления для уровня цен на мясо говядины для 80, получим значение уровня потребления равное 59,05 кг, т.е. с вероятностью 95% можно предполагать, что прогнозное значение будет находиться в интервале от 56,86 до 61,25. (Рисунок 5)

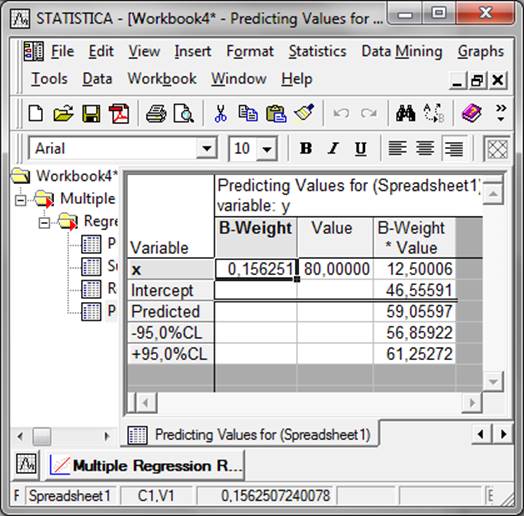
Рисунок 5 – Прогнозное значение уровня потребления

Таким образом, в результате проведения корреляционно-регрессионного анализа показано, что между уровнем цен на продукты питания и уровнем потребления существует тесная связь. Изучаемые признаки связаны линейной корреляционной зависимостью. Найдены параметры этой зависимости. Проведена комплексная оценка значимости, как параметров регрессионного уравнения, так и регрессии в целом. Следовательно, регрессионная модель зависимости цен на продукты питания и уровень потребления может быть использована для принятия управленческих решений.

 

Заключение