Педагогика \ Педагогика

Технологии проблемного обучения (преимущества и недостатки) при применении их на уроках в начальной школе, страница 7

№

Критерий

Уровни сформированности вычислительного навыка

1

Правильность

Ученик правильно находит результат арифметического действия над данными числами. Ребёнок иногда допускает ошибки в промежуточных операциях. Ученик часто неверно находит результат арифметического действия.

2

Осознанность

Ученик осознаёт, на основе каких знаний выбраны операции. Может объяснить решение примера. Ученик осознаёт на основе каких знаний выбраны операции, но не может самостоятельно объяснить, почему решал так.

3

Рациональность

Ученик, сообразуясь с конкретными условиями, выбирает для данного случая более рациональный приём. Может сконструировать несколько приёмов и выбрать более рациональный. Ученик, сообразуясь с конкретными условиями, выбирает для данного случая более рациональный приём, но в нестандартных условиях применить знания не может. Ребёнок не может выбрать операции, выполнение которых быстрее приводит к результату арифметического действия.

4

Обобщённость

Ученик может применить приём вычисления к большему числу случаев, то есть он способен перенести приём вычисления на новые случаи. Ученик может применить приём вычисления к большему числу случаев только в стандартных условиях. Ученик не может применить приём вычисления к большему числу случаев.

5

Автоматизм

Ученик выделяет и выполняет операции быстро и в свёрнутом виде. Ученик не всегда выполняет операции быстро и в свёрнутом виде. Ученик медленно выполняет систему операций, объясняя каждый шаг своих действий.

6

Прочность

Ученик сохраняет сформированные вычислительные навыки на длительное время. Ученик сохраняет сформированные вычислительные навыки на короткий срок. Ребёнок не сохраняет сформированные вычислительные навыки.

Для изучения уровня сформированности вычислительного навыков в контрольном и экспериментальном классах был проведен математический диктант:

1) из какого числа надо вычесть 700, чтобы получить 2500? 

2) какое число надо разделить на 500, чтобы получить 35? 

3 ) из чисел 500, 4, 160584, 80, 160000 составь одно равенство, используя только действие сложение (числа записываются на доске) 

4) увеличь 5228 в 100 раз. 

5) сколько центнеров в 5т 800 кг? 

6) на сколько надо разделить 660, чтобы получить 2200? 

7) из чисел 2928, 4691, 7882, 2001, 5375, 9749, 2807, 7983 выпиши числа наибольшее и наименьшее. Отыщи их разность и произведение (числа записываются на доске).

8) запиши все числа от 42153 до 52586, которые делятся на 100 без остатка.

Оценки, полученные за данный математический диктант, приведены в приложениях 1 и 2. Сводные итоги оценки уровня вычислительных навыков учащихся 4 «а» класса сведем в таблицу 4. 

                                  Таблица 4

Уровень  вычислительных навыков учащихся 4 «а» класса

Оценка

Кол-во учащихся

Кол-во учащихся  в %

2

6

30

3

10

50

4

3

15

5

1

5

По данным таблицы 4 построим диаграмму (рис.1)

Кол-во уч-ся в %

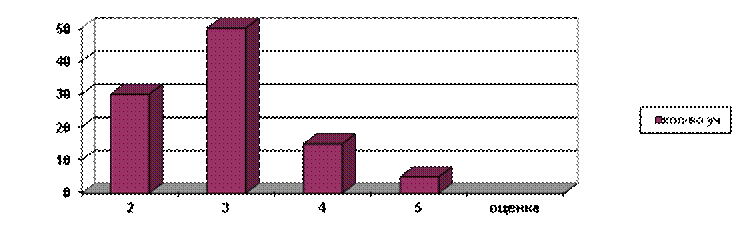
Рис. 1 Уровень  вычислительных навыков учащихся 4 «а» класса

Проанализировав диаграмму (рис.1), мы видим, что кол-во учащихся, имеющих двойку -  6 человек, тройку имеют 10 человек. Четверки имеют только 3 ученика, пятерки – 1 ученик. Таким образом, очевидно, что необходимо   проводить работу по  формированию вычислительных навыков. Также был определен уровень вычислительных навыков учащихся 4 «в» класса   (таблица 5).

Таблица 5

Уровень вычислительных навыков учащихся 4 «в» класса

Оценка

Кол-во учащихся

Кол-во учащихся  в %

2

3

15

3

7

35

4

6

30

5

5

20
Скачать файл