Математические методы теории принятия решений: Курс лекций, страница 20

Ввод ограничений на отыскиваемые переменные (B3, C3, D3) осуществляется следующим образом.

СЕРВИС, ПОИСК РЕШЕНИЯ. В окне Поиск решения установить целевую ячейку $C$8, равной минимальному значению. Изменяемые ячейки: $B$3:$D$3.

Ограничения:  B3 => B4; C3 => C4; D3 => D4;

B3 <= B5; C3 <= C5; D3 <= D5;

B3 = 1; C3 = 1; D3 = 1; {первоначально}

D9 = F9.

Формат/ Ячейки/ Число. Назначить две цифры после запятой.

Параметры поиска решения. В информационной строке Линейная модель флажок не ставить, нажать клавишу ОК.

ВЫПОЛНИТЬ. Нажать ОК. На экране окно Результаты поиска решения. Эти результаты показаны в таблице выделенным шрифтом.

Результаты поиска решения содержат отчеты по результатам и по устойчивости. Отчет по устойчивости состоит из двух таблиц.

В первой части таблицы приведены оптимальные значения переменных B3, C3, D3 и значение нормированного градиента (параметра поиска).

Во второй части таблицы приведены значения критерия оптимальности C8 = 227,93 и множителя Лагранжа  = 0,564. Последнее значение означает, что при дополнительных потребностях промышленного узла на каждую единицу новой мощности потребуется израсходовать 0,564 тонны топлива.

Подчеркиваем еще раз, что цифры в круглых скобках на рис.5 указывают на минимальные расходы топлива для каждой ТЭС, обеспечивающие оптимальную выработку располагаемых мощностей.

Рассмотренная нелинейная задача оптимизации является представителем целого класса задач энергосберегающих технологий. В данном случае речь шла о сбережении тепловой энергии сжигаемого топлива для производства требуемого количества электрической энергии, используемой в промышленных целях.

Приведем пример, когда функция Лагранжа используется для оценки развития промышленных объектов [1].

Пример. Для каждого из трех реконструируемых заводов известна зависимость капитальных вложений К от планируемого прироста продукции V:

K₁ = 0,1×V₁/(5 - V₁);

K₂ = 0,15×V₂/(6 – V₂);

K₃ = 0,12×V₃/(4 – V₃).

Требуется разработать оптимальный план реконструкции с минимальными капитальными затратами, обеспечивающий прирост производства 3 тыс. тонн в год.

РЕШЕНИЕ

1.  Составим целевую функцию – минимизация капитальных затрат:

F = K₁ + K₂ + K₃ ® min                  (1)

2.  Общий прирост производства строго ограничен директивным заданием:

V₁ + V₂ + V₃ = 3                      (2)

3.  Составим функцию Лагранжа:

L = F - l×(3 - V₁ - V₂ - V₃ ) ® min          (3).

4.  Подставим значения V₁, V₂ ,V₃ из выражения (2) в (3) и возьмем частные производные функции Лагранжа по переменным V_i, приравняв производные, равными нулю. Тогда получим зависимости, связывающие оптимальные значения V_i* с множителем Лагранжа l:

 ;

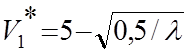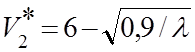 ;                        (4)

 .

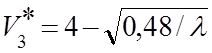5.  Подставив значения V_i* в ограничения (2), найдем оптимальное значение l* = 0,0383 ден. единиц / ед. ресурса. То есть на каждую денежную единицу прироста производства произойдет увеличение вкладываемого капитала на 0,0383 денежные единицы.

6.  Вернувшись к соотношениям (4) и подставив найденную величину l*, получим следующие оптимальные значения прироста производства по каждому заводу: V₁* = 1,388 тыс. тонн, V₂* = 1,154 тыс. тонн, V₃* = 1,458 тыс. тонн в год.

7.  Оптимальные значения V_i* входят в целевую функцию (1), минимизирующую капитальные годовые затраты, которые составят около 0,0895 ден. единиц. С учетом реального масштаба исходных данных это составит 89500 денежных единиц капитальных затрат.

Задачи оптимизации производства

В начале темы 4 уже назывались ключевые вопросы, контролирующие развитие экономики. Укажем на важный математический инструментарий, позволяющий сводить задачи условной оптимизации к безусловным задачам: это метод Лагранжа.

Для производственной функции f(x₁, x₂) любого вида и ограничений в форме равенства j(x₁, x₂) = b конструируется функция Лагранжа:

L(x₁, x₂, l) = f(x₁, x₂) +l×[b - j(x₁, x₂)] ® extr ,