Информатика и выч. техника \ Программирование

Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 36

Коэффициенты  a, b, c  взять из , полученного в задаче № 8.

Основа метода Эйлера

В основе метода численного интегрирования дифференциальных уравнений первого порядка по Эйлеру лежит замена первой производной искомой функции ее конечной разностью первого порядка, деленной на шаг по независимой переменной (времени)

Подставим заданные начальные значения  в полученное разностное выражение и разрешим его относительно . Результатом и будет формула интегрирования Эйлера:

Формулы итерационного процесса по Эйлеру

        €„            €    2       ‚†            ‚

ITERATES¦¦v +ht,v +ht·¦a·v  +b·v +c¦¦,v,[t0,x0],5¦

        … 1     2       2     2  ƒ‡            ƒ

NotationDigits:=6

                 2                   

f(x):=-0.434523·x +1.13628·x-0.420483

ITERATES(„v +0.1,v +0.1·f(v )†,v,[0,0],5)

         … 1      2        2 ‡           

„  0        0     †

¦ 0.1  -0.0420483 ¦

¦ 0.2  -0.0889512 ¦

¦ 0.3   -0.14145  ¦

¦ 0.4   -0.200441 ¦

… 0.5   -0.267011 ‡

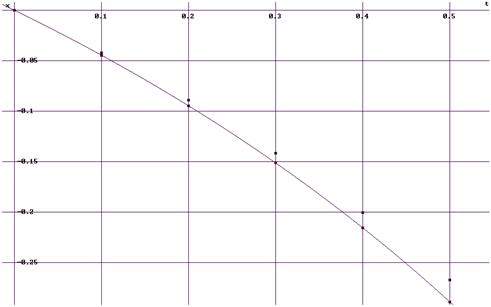
Сравнивая полученную таблицу с таблицей аналитического решения в задаче №19 можно заметить, что значения в ней имеют погрешность, пропорциональную величине шага по времени в первой степени (см. рис.).

Задача №21: Решение методом Рунге-Кутта

Методом Рунге-Кутта четвертого порядка в интервале [0,0.5] ([0,0.05]) с шагом  h=0.1 (0.01) получить решение нелинейного дифференциального:

Коэффициенты a,b,c взять из , полученного в задаче № 8. Сравнить таблицы решений задач 19, 20, 21  и сделать выводы по точности решения и ее зависимости от величины шага.

Соотношения к формуле интегрирования Рунге-Кутта

Формулы Рунге-Кутта различных порядков получаются путем вычисления взвешенного среднего приращения, составленного из прямых (Эйлеровых) и их итерационных приращений функции, полученных для нескольких удаленных точек. Наиболее популярной Формулой Рунге-Кутта является формула 4-го порядка точности, в которой значения функции вычисляются на расстоянии целого и половинного шагов по независимой переменной. При этом для половинного шага значение функции уточняется итерационной процедурой. При усреднении приращениям в средней точке придается вдвое больший вес:

где          – значение производной в начальной точке;

 – то же – в точке половинного шага;

 – итерационное уточнение в средней точке;

 – значение производной в конечной точке.

Построение итерационной процедуры Рунге-Кутта

NotationDigits:=6

                   2                   

f(t,x):=-0.434523·x +1.13628·x-0.420483

k1(v,h):=f(v ,v )

            1  2

          €    h      h         ‚

k2(v,h):=f¦v +——-,v +——-·k1(v,h)¦

           1  2   2  2         ƒ

          €    h      h         ‚

k3(v,h):=f¦v +——-,v +——-·k2(v,h)¦

           1  2   2  2         ƒ

k4(v,h):=f(v +h,v +h·k3(v,h))

            1    2           

          h                                       

f(v,h):=——-·(k1(v,h)+2·k2(v,h)+2·k3(v,h)+k4(v,h))

          6                                       

Rng(v0,h,n):=ITERATES(„v +h,v +f(v,h)†,v,v0,n)

                      … 1    2        ‡        

Rng([0,0],0.1,5)

„  0        0     †

¦ 0.1  -0.0445590 ¦

¦ 0.2  -0.0946778 ¦

¦ 0.3   -0.151296 ¦

¦ 0.4   -0.215575 ¦

… 0.5   -0.288961 ‡

Сравнивая вычисление по формуле Рунге-Кутта 4-го порядка с таблицей аналитического вычисления с 6 значащими разрядами можно заметить лишь кое-где отличие в последней цифре. Согласно теоретическим исследованиям погрешность этого метода пропорциональна 4-й степени шага.

Рассмотренные формулы численного интегрирования предполагают, что в интервале интегрирования искомая функция не терпит разрывов. Если такое случится с предлагаемыми вариантами числовых данных, то студентам необходимо взять другой интервал для интегрирования уравнения как методом Эйлера, так и методом Рунге-Кутта. В условии задачи другие значения интервала приведены в скобках.

Задача №22: Численное интегрирование системы

Скачать файл