Информатика и выч. техника \ Программирование

Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 25

Для построения многочлена Ньютона необходимы узловые многочлены со степенями от i=1 до i=n  и конечные разности таких же порядков. Последние представлены на второй строке исходной таблицы Tr в столбцах j , изменяющихся от j=3 до j=3+n.

Узловой многочлен можно сформировать следующим текстом в командной строке:

£(x - Tr™(1 + i)™1, i, 1, j)

Полученное выражение узлового многочлена степени j умножим на разделенную разность соответствующего порядка и просуммируем все слагаемые вместе с начальным значением табличной функции:

                     n             j                 

Pol_N(n) := Tr    +  ¤  Tr       · £  (x - Tr       )

              2,2   j=1   2,2 + j i=1        1 + i,1

Для вывода интерполяционного многочлена 3 степени в требуемом степенном формате в командной строке наберем и исполним следующий текст оператора:

APPROX(EXPAND(Pol_N(3), Trivial, x), 6)

          3            2                      

0.712961·x  - 4.35831·x  + 7.72024·x - 3.57314

Полученный многочлен Ньютона полностью соответствует многочлену Лагранжа. Заметное отличие в последних разрядах коэффициентов вызвано ограниченной точностью разделенных разностей и вычислениями по различным формулам с разрядностью, равной 6.

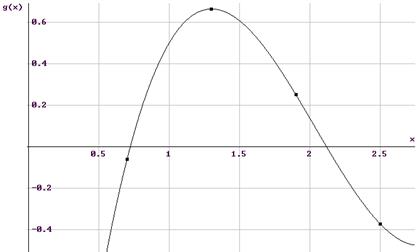
Кривая интерполяционных многочленов с заданными точками

Задача №7: Выражения для производных

Вывести выражения для вычисления второй производной в точке  в виде функций:

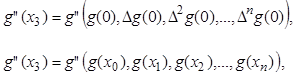
где          и  для n = 0,1,...,5  соответственно значения разностей в точке  и ординаты  из задачи №2. Значения  производной, вычисленные по выведенным формулам, сравнить с вычисленным значением производной, найденной путем дифференцирования интерполяционного многочлена G(x):

Соотношения для операторов дифференцирования

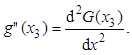
Между линейными операторами дифференцирования и операторами повторных конечных разностей «вперед» для таблично заданной функции существует следующее соотношение:

 

или иначе:

,

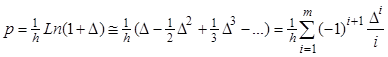где          – оператор дифференцирования непрерывной функции  

действительной переменной х;

 – определение оператора повторной конечной разности k-того порядка для таблично задаваемой функции с шагом h.

Значение производной n-го порядка в точке , расположенной на k-той строке (k=0,1,…) табличной функции, можно представить так:

Чтобы найти выражение n-й производной в заданной точке xk в виде функции от повторных конечных разностей, необходимо выполнить произведение многочленов, стоящих в квадратных скобках, относительно степеней конечно-разностных операторов и отбросить все слагаемые, порядок операторов которых выше максимального порядка m повторной конечной разности для таблично заданной функции.

Для получения выражения этой же производной с ординатами табличной функции, необходимо вместо каждой повторной конечной разности подставить их выражения с ординатами функции и сгруппировать подобные члены. Повторная разность i-того порядка () для начальной строки табличной функции  () через ее ординаты выражается следующим образом (см. выражение для S(m,j) в задаче №2):

Решение задачи

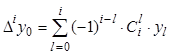
Исходные данные с шестью значениями табличной функции и ее пятью конечными разностями возьмем из задачи №2 в форме таблицы Tkr и интерполяционный многочлен  G(x)  из задачи №3.

В данной задаче заданы n = 2, k = 3 и максимальный порядок разностей m = 5. Шаг по целочисленной переменной в Tkr равен 1, а по действительной переменной x равен h=0.6.

Первая форма разностного выражения производной

Определим многочлены с заданными n, k, m и выполним умножение многочленов:

                 i           

            m   d       i - 1

p(d, m) :=  ¤  ————·(-1)     

           i=1   i           

                k

E(k) := (1 + d )

                                  n             

Md(n, k, m) := EXPAND(E(k)·p(d, m) , Trivial, d)

Md(2, 3, 5)

Для обращения в ноль слагаемых развернутого многочлена с повторными разностями порядков выше m=5 поступим следующим образом. Продифференцируем(j+1) раз полученный многочлен Md(n, k, m) по переменной d, после чего (j+1) раз по этой же переменной выполним интегрирование. Это обратит в нуль все слагаемые со степенями переменной d от 0 до (j+1). Вычитая из полного многочлена многочлен, у которого обнулены слагаемые со степенями ниже (j+1), мы получим многочлен со степенями слагаемых до (j+1).

Скачать файл