Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 22

     … 5  3.7   -1.94    ""      ""      ""     ""     ""  ‡

Факториальный многочлен -ой степени для аргумента  имеет вид:

            n!   

fm(n,k):=———————- .

          (n-k)!

VECTOR(fm(n,k),k,0,3)  [1,n,n·(n-1),n·(n-1)·(n-2)]

В таблице Tkr необходимо выделить вторую строку и использовать значения конечных разностей от нулевого порядка, которая находится на 3 месте, до 5 порядка, которая находится на 8 месте. Таким образом, интерполяционный многочлен от табличной функции с целочисленным аргументом на основе факториальных многочленов можно представить так:

                                  Tkr      

      DIMENSION(Tkr™2)-3             2,3+k

P(n):=        ¤          fm(n,k)·—————————-

             k=0                     k!    

Чтобы привести P(n) к его степенной форме с 6 десятичными знаками у коэффициентов, используем  команды  EXPAND  и  APPROX :

Pol(n):=APPROX(EXPAND(P(n),Trivial,n),6)

           5           4          3          2             

0.0193333·n -0.240833·n +1.11566·n -2.51916·n +2.349·n-0.06

Переход к полиному с действительным аргументом осуществим путем подстановки  в качестве фактического параметра в Pol(n) :

   € x-0.7 ‚

Pol¦——————-¦

     0.6  ƒ

        5          4          3          2

G(x)=0.248628·x -2.72847·x +11.5865·x -24.1605·x +

+24.1524·x-8.48893

Построенные интерполяционные многочлены изобразим в виде графиков с нанесенными на них точками из таблицы. Для нанесения точек на график таблично заданные функции целого и действительного аргументов необходимо представить в форме матриц с двумя столбцами.

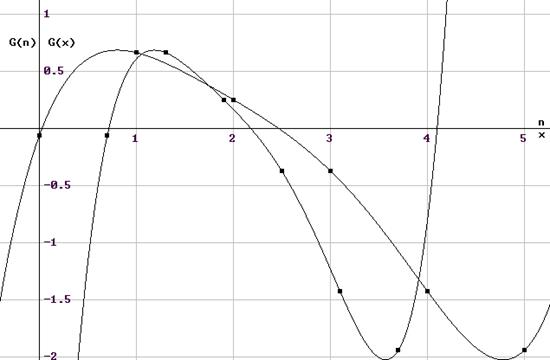
Такие матрицы сформируем из вектора G, удалив не нужную векторную компоненту и выполнив транспонирование результата:

Высвечивая курсором интерполяционный многочлен и его таблицу поочередно в графическом режиме вычертим кривую с нанесенными на нее точками. Вид этих графиков приведен на рисунке ниже.

DELETE_ELEMENT(G,2)` „ 0   -0.06 † ¦ 1   0.664 ¦ ¦ 2   0.252 ¦ ¦ 3  -0.372 ¦ ¦ 4  -1.424 ¦ 5   -1.94 ‡

DELETE_ELEMENT(G,1)` „ 0.7   -0.06 † ¦ 1.3   0.664 ¦ ¦ 1.9   0.252 ¦ ¦ 2.5  -0.372 ¦ ¦ 3.1  -1.424 ¦ 3.7   -1.94 ‡

Задача 4: Суммирование функциональных рядов

Вывести аналитическое выражение суммы 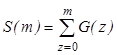 для функции целочисленного аргумента G(z). Проверить правильность полученного выражения прямым суммированием табличных значений G(k), k=0, 1, 2, 3, 4, 5    (m=5).

Теоретические предпосылки

Суммирование конечных разностей некоторой функции в пределах от a до b связано с необходимостью поиска функции, породившей конечные разности:

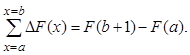
Известно, что факториальный многочлен k-того порядка выражается через конечную разность факториального многочлена (k+1)-го порядка так:

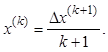
Если суммируемую функцию разложить в ряд по факториальным многочленам разных степеней (от 0 до n), то каждое слагаемое в этом разложении можно заменить конечной разностью от факториального многочлена с порядком на единицу большим. Теперь можно представить суммирование i-того слагаемого разностью первообразных, в которые вместо аргумента х подставлены значения пределов суммирования:

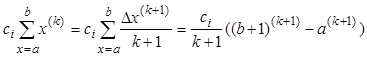
Таким образом, суммирование в пределах a“z“b функции целочисленного аргумента  в результате описанных преобразований и подстановок можно представить в следующем виде:

.

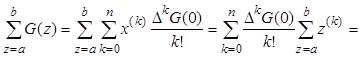
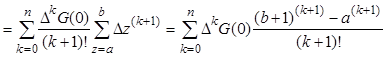Формула суммирования в пределах от 0 до m ординат табличной функции, которая заданна лишь (n+1)-й строкой, будет выглядеть так:

.

Разработка вычислительных операторов

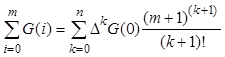В качестве исходных данных будем использовать таблицу Tkr из предыдущих задач для выборки из нее значений исходной функции и разностей всех порядков .

„      € fm(m+1,k+1)       ‚†

¦VECTOR¦————————————-,k,0,5¦¦`

…           k+1           ƒ‡

В качестве проверки этот оператор перечисляет суммы конечных разностей от факториальных многочленов всех порядков, начиная с первого, в пределах [0, m]:

„                    m+1                   †

¦                0.5·m·(m+1)               ¦

¦          0.333333·m·(m+1)·(m-1)          ¦