Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 40

Собственные значения и собственные векторы матрицы

Собственными значениями  квадратной матрицы А размера  являются числа, удовлетворяющие векторному равенству . Находятся собственные значения путем решения характеристического уравнения .

Собстенным вектором  матрицы А является вектор, получаемый в результате решения однородной системы уравнений . Из множества решений этой системы берется лишь вектор, имеющий норму (длину) равную единице. Важнейшим свойством собственных векторов являются их линейная независимость и взаимная ортогональность.

Упомянутыми свойствами собственных векторов наделены векторы y1,y2,y3 , сформированные в задаче №23. Поэтому эту систему векторов можно считать системой левосторонних (строчных) собственных векторов некоторой, пока неизвестной матрицы. Транспонированная ортогональная матрица, она же обратная, состоит из тех же нормированных векторов, но представленных в матрице столбцами.

Функции с матричным аргументом

Вычисление функций с матричкым аргументом выполняется путем ее разложения на сумму слагаемых с матричным коэффициентом, умноженным на функцию, аргументом которой является собственное значение. Матричные коэффициенты называют проекторами матрицы.

Разложение называют спектральным, то есть по всему спектру (составу) собственных значаний:

,

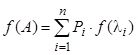где          – собственные значения матрицы А;

                – проектор матрицы – матрица размера , получаемая путем матричного умножения собственного вектора самого на себя.

Матричное умножение векторов осуществляется по правилам умножения двух прямоугольных матриц: матрицы размера  на матрицу размера .

Решение поставленной задачи

Система ортонормированных векторов из 23 задачи:

y1:=[-0.0841820,0.931614,0.353564]

y2:=[-0.380545,0.297868,-0.875476]

y3:=[0.920922,0.208247,-0.329446]

NotationDigits:=6

P1:=[y1]`•[y1]

    „ 0.00708661  -0.0784251  -0.0297637 †

P1:=¦ -0.0784251   0.867905    0.329385  ¦

    … -0.0297637   0.329385    0.125007  ‡

P2:=[y2]`•[y2]

    „ 0.144815   -0.113352  0.333158  †

P2:=¦ -0.113352  0.0887259  -0.260777 ¦

    … 0.333158   -0.260777  0.766459  ‡

P3:=[y3]`•[y3]

    „ 0.848098    0.191779    -0.303394 †

P3:=¦ 0.191779    0.0433669  -0.0686063 ¦

    … -0.303394  -0.0686063   0.108535  ‡

Сумма всех проекторов матрицы есть единичная матрица:

P1+P2+P3

„                         -6            -7 †

¦   0.999999    1.57030·10    4.09104·10   ¦

¦           -6                          -6 ¦

¦ 1.57030·10      0.999998    2.26953·10   ¦

¦           -7            -6               ¦

… 4.09104·10    2.26953·10       1.00000   ‡

Заданные собственные значения равны .

Используя формулу спектрального разложения, получим матрицу А и ей обратную А_1:

A:=P1·(-1)+P2·(-2)+P3·(-3)

„ -2.84101   -0.270207  0.273630 †

¦ -0.270207  -1.17545   0.397987 ¦

… 0.273630   0.397987   -1.98353 ‡

          1       1       1

A_1:=P1·———-+P2·———-+P3·———-

         -1      -2      -3

„  -0.362193  0.0711750  -0.0356840 †

¦  0.0711750  -0.926724   -0.176128 ¦

… -0.0356840  -0.176128   -0.544415 ‡

Произведение этих матриц должно дать матрицу единичную:

A•A_1

„                         -6            -6 †

¦   0.999999    4.94942·10    1.68133·10   ¦

¦           -6                          -6 ¦

¦ 2.40680·10      0.999996    2.99902·10   ¦

¦           -7            -6               ¦

… 2.56919·10    7.12614·10       1.00000   ‡

В качестве еще одной проверки найдем характеристическое уравнение и собственные значения полученной матрицы А:

   €    „ 1  0  0 †‚

DET¦A-¿·¦ 0  1  0 ¦¦

       … 0  0  1 ‡ƒ

           3          2                  

-0.999996·¿ -5.99997·¿ -10.9999·¿-5.99997

     €   €    „ 1  0  0 †‚  ‚

SOLVE¦DET¦A-¿·¦ 0  1  0 ¦¦,¿¦

            … 0  0  1 ‡ƒ  ƒ

[¿=-3.00000,¿=-2.00000,¿=-0.999999]

Задача №25: Решение системы уравнений

Решить систему линейных уравнений , где A – матрица коэффициентов, полученная в задаче № 24,  – вектор решения,  – вектор правых частей. Решение получить следующими методами:

а) используя преобразование матрицы A в диагональную D;

б) используя обратную матрицу, полученную в задаче № 24;