Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 33

	35	-104	114	-56	11	-150 ,  12
	11	-20	6	4	-1	15 ,  -3
	-1	16	-30	16	-1	0 ,   2
	-1	4	6	-20	11	15 ,   3
	11	-56	114	-104	35	150 , -12

На рисунке показано расположение аппроксимирующих 5-точечных интервалов у отдельных участков рассматриваемого стержня. Жирным пятном на них отмечены номера тех точек, для которых из таблицы выбираются аппроксимирующие выражения для второй производной.

Для рассматриваемой задачи должны быть вычислены вторые производные для 6 внутренних точек, следовательно аппроксимирующая система будет состоять из 6 дифференциальных уравнений первого порядка. Коэффициент пропорциональности между аппроксимирующим выражением и частной производной приведен в левом верхнем углу таблицы.

Расположение аппроксимирующих интервалов.

В общем виде система дифференциальных уравнений будет такой:

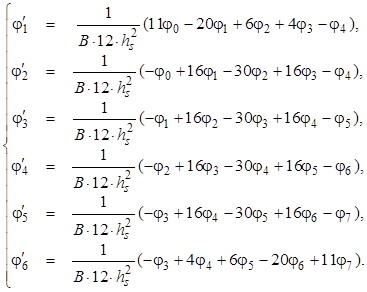
Значения функции на границах стержня заданы: . Начальные значения функции  в заданных точках на стержне для выбранной  вычислим следующим образом:

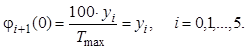
Решение этой системы будет получено в задаче №22.

Задача № 17: Вычисление корней уравнения

Используя метод Ньютона-Рафсона, найти с относительной погрешностью в одну миллионную нуль многочлена Чебышева , полученного в задаче № 14. В качестве начального приближения к корню взять

 .

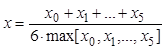В качестве  берутся || из таблицы исходных данных.

Решение задачи

В качестве исходных данных для вычисления начального приближения сформируем вектор из заданных ординат табличной функции:

y:=[-0.06,0.664,0.252,-0.372,-1.424,-1.94]

      6       

      ¤  ¦y ¦

     i=1 ¦ i¦

x0:= —————————-        1.182730

     6·MAX(y)

В 14-й задаче был получен многочлен Чебышева 4-й степени:

f(x):=COS(4·ACOS(x))

или

         4    2  

f(x):=8·x -8·x +1

Итерационный процесс Ньютона можно представить следующим оператором:

„        €      f(x)           ‚†

¦ITERATES¦x-———————————-,x,x0,6¦¦`

¦        ¦   €d ‚1             ¦¦

¦        ¦   ¦——¦  f(x)        ¦¦

…           dxƒ              ƒ‡

Количество итераций выбираем равное 6, так как сходимость этого процесса в большинстве случаев близка к сходимости геометрической прогрессии, которая с каждой итерацией уменьшает погрешность в среднем примерно на порядок. По условию задачи вычисление необходимо провести с точностью в одну миллионную, то есть на 6 порядков уменьшить погрешность, полученную при подстановке начального значения. Правда, в зависимости от конкретного вида функции могут наблюдаться отклонения в сторону большего числа итераций или даже расходимость процесса.

„ 1.182730  †

¦ 1.022130  ¦

¦ 0.9450152 ¦

¦ 0.9251660 ¦

¦ 0.9238847 ¦

¦ 0.9238795 ¦

… 0.9238795 ‡

Как видим уже на 6-й итерации результат начал повторяться. Подставим полученное значение корня в исходное уравнение, чтобы убедиться что найденное значение действительно приближает значение функции к нулю:

                         -7

f(0.9238795)=-3.398243·10  

Задача №18: Решение нелинейной системы

Методом Ньютона-Рафсона найти решение системы нелинейных алгебраических уравнений, полученных в задаче № 10в. Корни системы получить с четырьмя верными знаками.

Построение итерационного процесса

Представим систему уравнений с 4 неизвестными (w0,w1,x1,x2), которые в задаче №10в представляли параметры квадратурной формулы, в виде вектора f. Компонентами этого вектора должны быть неявные формы уравнений:

   „      -2+w0+w1      †

   ¦     w0·x1+w1·x2    ¦

   ¦   2       2      2 ¦

f:=¦ -——-+w0·x1 +w1·x2  ¦

   ¦   3                ¦

   ¦         3      3   ¦

   …    w0·x1 +w1·x2    ‡

Решением этой системы окажется вектор V:=[w0,w1,x1,x2], компонентам которого должны быть числовые значения, с заданной точностью удовлетворяющие системе.