Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 35

Скорость изменения переменной x(t) во времени равна функции от этой переменной f(x). Найти аналитическое выражение последней от времени, начиная с t=0, если в начальный момент x(0)=0. В качестве f(x) взять степенной многочлен , полученный в задаче № 8. Полученное решение протабулировать с шагом h=0.1 (0.01) в интервале [0,0.5] ([0,0.05]).

Получение аналитического решение уравнения

В условии задачи сказано, что производная по времени от искомой функции равна многочлену 2-й степени от нее же, что можно записать так:

,

где         a, b, c – коэффициенты аппроксимирующего многочлена 2-й степени из задачи № 8, которые для данного случая соответственно равны:

a= -0.434523;  b = 1.13628;  c = -0.420483.

Данное уравнение относится к классу дифференциалных уравнений с разделяющимися переменными и начальными условмями. В нотации пакета DERIVE запишим неявную форму уравнения с разделенными переменными, в которую войдут интегралы с переменным пределом от левой и правой частей. В командной строке и на поле операторов это будет выглядеть так:

INT(1/(a·x^2+b·x+c),x,x0,x) - INT(1,t,t0,t)

x                  t      

ˆ         1         ˆ       

¦   ———————————- dx - ‰   1 dt

¦       2            t0     

‰    a·x +b·x+c       

 x0                    

Общее выражение в результате интегрирования имеет вид

       €   2·a·x+b   ‚         €   2·a·x0+b  ‚      

 2·ATAN¦————————————-¦   2·ATAN¦————————————-¦      

       ¦          2  ¦         ¦          2  ¦      

        ‹(4·a·c-b ) ƒ          ‹(4·a·c-b ) ƒ      

——————————————————————--——————————————————————--t+t0

               2                       2            

      ‹(4·a·c-b )             ‹(4·a·c-b )           

Математический пакет дает возможность в символьном виде разрешить этот результат относительно переменной x, в которое все равно необходимо будет подставить конкретные числовые значения, поэтому такую подстановку в оператор SOLVE() сделаем заранее:

   €     € x                                       t       ‚‚

   ¦     ¦ˆ                  1                    ˆ        ¦¦

RHS¦SOLVE¦¦  ————————————————————————————————- dx-‰  1 dt,x¦¦

   ¦     ¦¦              2                         0       ¦¦

   ¦     ¦‰   -0.434523·x +1.13628·x-0.420483              ¦¦

         0                                               ƒƒ

Полученное решение включает условное выражение, которое в общем символьном решении было вызвано необходимостью проверки знака дискриминанта, составленного из коэффициентов квадратного уравнения:

„  €                       21   0.748527·t        ‚†

¦  ¦             1.09997·10  ·(ê          -1)     ¦¦

¦IF¦-1<0“1,——————————————————————————————————————-¦¦

¦  ¦                  20  0.748527·t           21 ¦¦

…          5.07174·10  ·ê          -2.46530·10   ƒ‡

Исполнив условный оператор, получим окончательную формулу для функции времени, являющейся решением заданного уравнения:

„               5   0.748527·t        †

¦     5.49985·10 ·(ê          -1)     ¦

¦————————————————————————————————————-¦

¦           5  0.748527·t           6 ¦

… 2.53587·10 ·ê          -1.23265·10  ‡

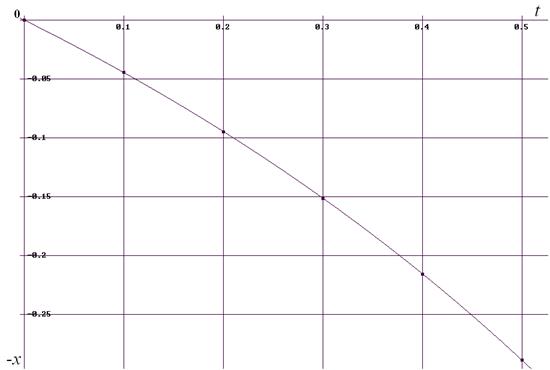
График этого решения, показанный ниже, в области заданного интервала изменения времени [0, 0.5] не содержит особенности, поэтому его табуляцию проведем с шагом  h=0.1.

      €„                 5   0.748527·t        †            ‚

      ¦¦       5.49985·10 ·(ê          -1)     ¦            ¦

VECTOR¦¦t,————————————————————————————————————-¦,t,0,0.5,0.1¦

      ¦¦             5  0.748527·t           6 ¦            ¦

      …   2.53587·10 ·ê          -1.23265·10  ‡            ƒ

„  0        0     †

¦ 0.1  -0.0445589 ¦

¦ 0.2  -0.0946777 ¦

¦ 0.3   -0.151296 ¦

¦ 0.4   -0.215575 ¦

… 0.5   -0.288961 ‡

Полученные точки наносим на график. С этими аналитически полученными значениями будем сопоставлять результаты численного интегрирования в задачах 20 и 21.

Задача №20: Интегрирование методом Эйлера

Методом Эйлера в интервале [0,0.5] ([0,0.05]) с шагом h=0.1 (0.01) получить решение нелинейного дифференциального уравнения: