Информатика и выч. техника \ Программирование

Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 27

Недостатком интерполяционных многочленов является наличие у них большого числа экстремумов и точек перегибов, которые являются следствием многократного суммирования узловых многочленов , хотя сама табличная функция могла быть получена табулированием функции гладкой на заданном интервале.

Теоретические исследования физических процессов, данные измерения которых необходимо представить в аналитическом виде, всегда позволяют записать его обобщенную формулу, включающую несколько неизвестных параметров. Нахождение этих параметров, использующее критерий минимума среднего квадрата отклонения табличных данных от искомой аналитической зависимости, называют методом наименьших квадратов (МНК). Формула такого критерия близости имеет вид:

,

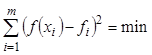где          – точка экспериментальных данных из таблицы,

 – значение искомой зависимости в точке .

Если искомую функцию представлять многочленом степени n, то неизвестными параметрами будут (n+1)коэффициент. Подстановка искомого многочлена в критерий близости образует функционал, зависящий от параметров.

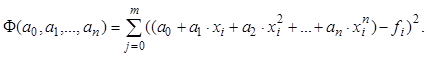
Минимум этого функционала находится в точке , где все частные производные функционала по параметрам равны нулю. Выполнив эти действия, получим систему линейных уравнений относительно неизвестных параметров :

где 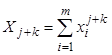         – постоянный коэффициент, равный сумме всех

значений аргументов со степенями (j+k);

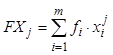 – числовые значения в правой части системы

линейных алгебраических уравнений;

n – количество данных в таблично заданной функции;

m – желаемая степень аппроксимирующего многочлена.

Построение таблицы для вычисления сумм

В качестве табличной функции для построения аппроксимирующего многочлена используем заданную функцию G(x) из задачи №2:

        „  0.7    1.3    1.9     2.5     3.1    3.7  †

G(x) := ¦                                            ¦

        … -0.06  0.664  0.252  -0.372  -1.424  -1.94 ‡

Для сокращения выводимых на экран и на печать записей процедур сделаем следующие установки и переименования:

DisplayFormat:=Compressed

D(A):=DIMENSION(A)

Вычисление вектора правых частей системы нормальных уравнений выполним следующим образом:

        D(G`)       €„         j-1†        ‚

Y(G,m):=  ¤   VECTOR¦¦G   ·G      ¦,j,1,m+1¦

         i=1        … 2,i  1,i   ‡        ƒ

Будем проверять функционирование процедур на примере построения аппроксимирующего многочлена степени m=3 :

Y(G,3)

„   -2.88  †

¦ -11.2224 ¦

¦ -40.5657 ¦

… -143.335 ‡

Вычисление матрицы коэффициентов системы нормальных уравнений:

        D(G`)       €      €    k+j-2        ‚        ‚

M(G,m):=  ¤   VECTOR¦VECTOR¦G        ,k,1,m+1¦,j,1,m+1¦

         i=1               1,i             ƒ        ƒ

M(G,3)

„    6      13.2     35.34   105.468 †

¦  13.2     35.34   105.468  334.958 ¦

¦  35.34   105.468  334.958  1106.02 ¦

… 105.468  334.958  1106.02  3749.36 ‡

Формирование вектора степеней аргумента табличной функции:

        „        j-1         †

X(x,m):=…VECTOR(x   ,j,1,m+1)‡

X(x,3)

„        2   3 †

… 1  x  x   x  ‡

Для получения вектора решения системы нормальных уравнений необходимо обратную матрицу коэффициентов умножить на вектор правых частей системы. Умножив скалярно вектор решения на вектор степеней переменной, получим выражение для аппроксимирующего многочлена:

                                               -1         

MNK_POL(G,m,x):=IF(m’D(G`),"m’n",X(x,m)•(M(G,m)  •Y(G,m)))

MNK_POL(G,3,x)

„           3          2                   †

… 0.331041·x -2.61948·x +5.34128·x-2.62084 ‡

Для построения одновременно аппроксимирующих многочленов всех заданных степеней и (для контроля правильности разработанных операторов) многочлена максимально возможной степени используем следующий оператор:

VECTOR((MNK_POL(G,m,x)) ,m,[0,1,2,3,5])

                       1               

Решения системы нормальных уравнений для высоких степеней из-за плохой меры обусловленности необходимо выполнять с разрядностью не ниже 12.  Вывод же на экран этих многочленов сделаем с 4 разрядами:

Скачать файл