Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 39

¦         -10  7         -7  6         -6  5         -7  4            3         -5  2                    -52 ¦

… 1.994·10   ·x +1.768·10  ·x -3.779·10  ·x +1.988·10  ·x +0.0003077·x -4.064·10  ·x -0.008787·x+6.920·10    ‡

Кривые, построенные по этим интерполяционным многочленам, показаны на рисунке ниже. 

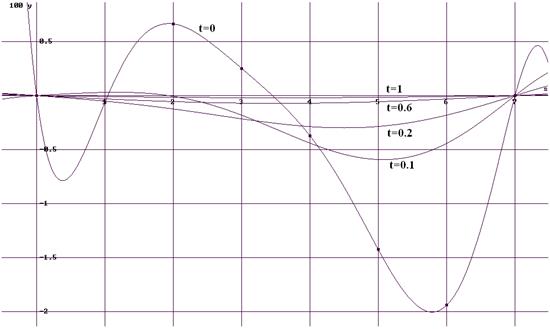
На кривую  t=0  нанесены точки начальных значений. Для этого необходимо исполнить таблицу координат, вырезанную из MM оператором

APPEND(„MM` †,„MM` †)`

       …   1‡ …   2‡  

Задача № 23: Ортонормирование векторов

Проверить заданную систему из трех векторов на линейную зависимость. При обнаружении линейной зависимости поменять местами первые компоненты векторов  (или , или ) и выполнить повторную проверку. Из исходных данных векторы формируются так:

 

На базе линейно независимой системы векторов  методом Грама-Шмидта построить ортонормированную систему трех векторов:

,   ,   .

На основе полученной системы векторов сформировать квадратную матрицу . Вычислить  и получить матрицы – обратную  и транспонированную . Найти произведения , . Сделать выводы о свойствах матрицы T.

Проверка линейной независимости векторов

Набор исходных векторов:

x1:=[-0.06,0.664,0.252]

x2:=[-0.372,-1.424,-1.94]

x3:=[0.6,0.7,0]

Для проверки системы векторов на линейную независимость достаточно проверить детерминант произведения двух матриц: матрицы из проверяемой системы векторов и матрицы транспонированной.

Mx:=[x1,x2,x3]

„  -0.06   0.664  0.252 †

¦ -0.372  -1.424  -1.94 ¦

…   0.6     0.7     0   ‡

DET(Mx•Mx`)

0.496585

Отличие от нуля свидетельствует о линейной независимости.

Построение ортонормированной системы векторов

Чтобы построить из линейно независимой системы векторов ортонормированную систему, необходимо сначала на их основе построить систему ортогональных векторов, а затем выполнить нормирование.

v1:=x1

v2:=x2+a21·v1

v3:=x3+a32·v2+a31·v1

Коэффициенты  a21, a32, a31 вычисляем из условия, что скалярное произведение ортогональных векторов равно нулю:

SOLVE(v1•v2,a21)

[a21=2.77971]

v2:=x2+2.77971·v1

[-0.538782,0.421727,-1.23951]

SOLVE([v1•v3,v2•v3],[ a32, a31])

[ a32=0.0139970  a31=-0.844094 ]

v3:=x3+0.013997·v2+(-0.844094)·v1

[0.643104,0.145424,-0.230061]

Для нормирования полученных ортогональных векторов каждый вектор необходимо разделить на его длину:

        v1    

y1:=—————————-

     ‹(v1•v1)

[-0.0841820,0.931614,0.353564]

        v2    

y2:=—————————-

     ‹(v2•v2)

[-0.380545,0.297868,-0.875476]

        v3    

y3:=—————————-

     ‹(v3•v3)

[0.920922,0.208247,-0.329446]

Ортогональная матрица и ее свойства

Объединив в единую матрицу ортонормированные векторы, получим ортогональную матрицу:

T:=[y1,y2,y3]

„ -0.0841820  0.931614  0.353564  †

¦  -0.380545  0.297868  -0.875476 ¦

…  0.920922   0.208247  -0.329446 ‡

Главным свойством ортогональной матрицы является равенство ее транспонированной и обратной матриц:

 -1

T  

„ -0.0841836  -0.380545  0.920922  †

¦  0.931615   0.297872   0.208246  ¦

…  0.353561   -0.875475  -0.329446 ‡

T`

„ -0.0841820  -0.380545  0.920922  †

¦  0.931614   0.297868   0.208247  ¦

…  0.353564   -0.875476  -0.329446 ‡

    -1

T`-T  

„           -6             -7             -9 †

¦ 1.62488·10     1.87902·10     2.71727·10   ¦

¦            -7             -6            -7 ¦

¦ -8.95687·10    -3.08518·10    3.48404·10   ¦

¦           -6              -6            -7 ¦

… 2.74694·10     -1.13136·10    2.27826·10   ‡

T•T`

„                           -6            -7  †

¦       1        -3.29002·10    4.04901·10    ¦

¦            -6                            -8 ¦

¦ -3.29002·10          1        -9.67120·10   ¦

¦           -7              -8                ¦

… 4.04901·10     -9.67120·10          1       ‡

Неравные нулю значения вызваны вычислениями с ограниченным числом разрядов. В данном случае вычисления проводились с 6 разрядами.

Задача №24: Проекторы матрицы

Считая числа –1, –2, –3 собственными значениями, а векторы  из задачи № 23 – собственными векторами некоторой матрицы A, найдите проекторы этой матрицы , саму матрицу A и ей обратную. Получить характеристическое уравнение матрицы A и подтвердить правильность всех промежуточных вычислений.