uu U1. 11. РЕГУЛЯРНЫЕ ФУНКЦИИ
Функция w==f(z), заданная на множестве Е и отображающая Е на Е', является однолистной на Е тогда и только тогда, когда обратная функция z=h(w) однозначна на множестве Е'.
2. Примеры однолистных отображений.
Пример 1. Линейная функция
w=/(z)=az+b, (1)
где а, Ь — комплексные постоянные (а ¥= 0), однолистна во всей комплексной плоскости, так как обратная функция
z=h(w)=-l-w--b- (2)
\ ' а а ' '
однозначна.
Функция (1) отображает взаимно однозначно расширенную комплексную плоскость z на расширенную комплексную плос
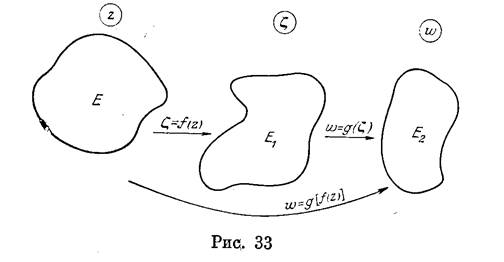
кость w. При этом точка z = °о переходит в точку w = °°, а соответствие между конечными точками плоскостей z и w определяется формулами (1), (2).
Рассмотрим случай 6=0. Тогда
w==az, (3) откуда
\w\ == lal Izl, arg w = arg a + arg z. (4)
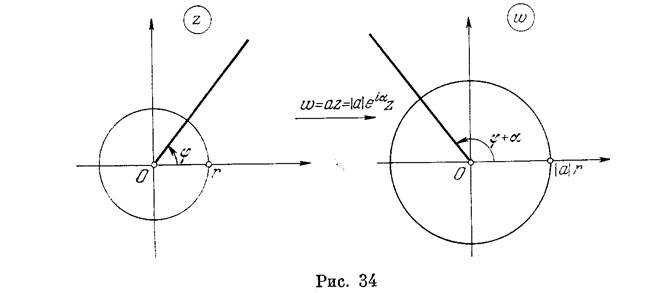
Из равенств (4) следует, что отображение (3) сводится к подобному растяжению плоскости z в lal раз с центром подобия в начале координат и повороту всей плоскости вокруг точки z = 0 на угол а = arg а. При отображении (3) луч arg z == (р переходит в луч argw=(p+a, а окружность |z|=r—в окружность \w\ = \а\г (рис. 34). Круг |z| <R при этом отображении переходит в круг \w\ < \a\R.
Если lal =1, т. е. а == е'°, то преобразование (3) есть поворот плоскости на угол а. В частности, преобразование w = iz есть
поворот на угол л/2, а преобразование w = —z есть поворот на угол я.
§ 8. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ 67
Преобразование (1) есть суперпозиция преобразований
S=la|z, т^е1"'", w=t+&.
Поэтому преобразование w = az + Ъ можно осуществить, выполнив в указанном порядке следующие преобразования:
а) подобное растяжение плоскости z в Ы раз (центр подобия — в точке 2=0);
б) поворот плоскости ^ вокруг точки t = 0 на угол а = arg а;
в) параллельный перенос (сдвиг) плоскости т на вектор
ъ. п
Пример 2. Функция
ц,=4 (5)
отображает взаимно однозначно расширенную комплексную плоскость z на расширенную комплексную плоскость w (обратная функция z == 1/w однозначна). При этом точке z=0 соответствует точка w = °°, а точке z = °° — точка w = 0. Луч arg г = (р переходит при отображении (5) в луч arg w = —<р, окружность Izl = г — в окружность \w\ == 1/г, круг |z| < R — на область
\w\>i/R. Q
Пример 3. Рассмотрим функцию
w=z\ (6)
Если z\ = z^, то либо Zi = г;, либо
Zi=-zz. (7)
Две точки, связанные равенством (7), симметричны относительно начала координат. Следовательно, функция w = z2, однолистна в области D в том и только в том случае, когда эта область не содержит ни одной пары точек, симметричных относительно точ-
;•>*
68 ГЛ. II, РЕГУЛЯРНЫЕ ФУНКЦИИ
кп 0. В частности, функция (6) однолистна в верхней полуплоскости Im z > 0.
Рассмотрим луч argz=a (0<а<я), лежащий в верхней полуплоскости (рис. 35). При отображении (6) этот луч переходит в луч arg w == 2ос. Будем вращать луч arg z == а, непрерывно увеличивая а от 0 до л. Тогда луч arg w = 2а, являющийся образом луча arg z == а, будет поворачиваться против часовой
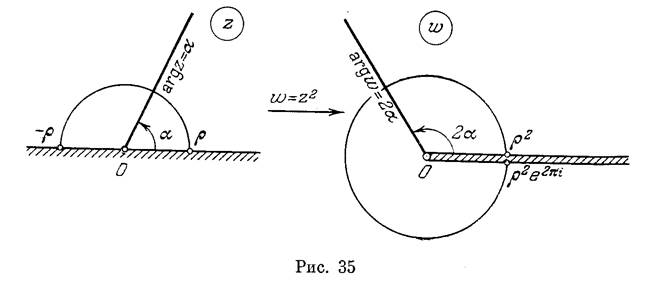
стрелки. Если луч на плоскости z опишет верхнюю полуплоскость, то его образ опишет всю плоскость w. При этом лучи argz=0 и argz==n, образующие границу области Im z > 0, перейдут соответственно в лучи arg w = 0 и arg w == 2л. Геометрически эти лучи совпадают с положительной действительной полуосью на плоскости w. Для того чтобы отображение (6) было взаимно однозначным не только внутри области Im z > 0, но и на ее границе, проведем в плоскости w «разрез» по положительной части действительной оси и будем считать, что луч arg z = О (т. е. положительная полуось на плоскости z) отображается на верхний, а луч arg z = л — на нижний берег этого разреза.
Итак, функция w = z2 однолистна в верхней полуплоскости и отображает эту область на плоскость w с разрезом вдоль положительной действительной полуоси (рис; 35). Отметим еще, что при отображении w == z3 полуокружность z = ре'6, 0 < 6 < л перейдет в «незамкнутую» окружность |гу|=р2 (точки Wi == р2 и Wi = рУ', являющиеся образами точек Zi = р и га = ре'" = —р, совпадают, но лежат на разных берегах указанного выше разреза).
Функция w = z2 является однолистной и в нижней полуплоскости и отображает область Im z < 0 на плоскость w с разрезом вдоль положительной действительной полуоси (рис. 36). При этом отображении лучи arg z = л и arg z = 2л, образующие границу области Im z < 0, переходят соответственно в верхний и нижний берега разреза. В самом деле, луч arg z = л+ б (б>0, б — достаточно мало), который «примыкает» к лучу argz==n, перехо-
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.