Математика \ Теория функций комплексного переменного

Регулярные функции. Дифференцируемые функции. Условия Коши — Римана. Геометрический смысл производной, страница 10

§ 8. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ            71

Za(ulo==f((J(to))==f(zo)). По правилу дифференцирования слож­ной функции

w'(t,)=f(z,)a'(t,).                    (Щ

Так как по условию f'(za)^0 и о'((о)^0 (см. § 3), то w'(?o)^ =7^0, т. е. кривая 'у' имеет касательную в точке Wa. Пусть argu/((o)= 6'. Тогда из (10) находим

О^ = arg w' (fo)- arg f (zo) + arg о' ((о),

9'=9+argf(z„).(11)'

Величина а = 9' — 9 называется углом поворота кривой ^ в точке Zo при отображении w=/(z). Из формулы (11) следует,

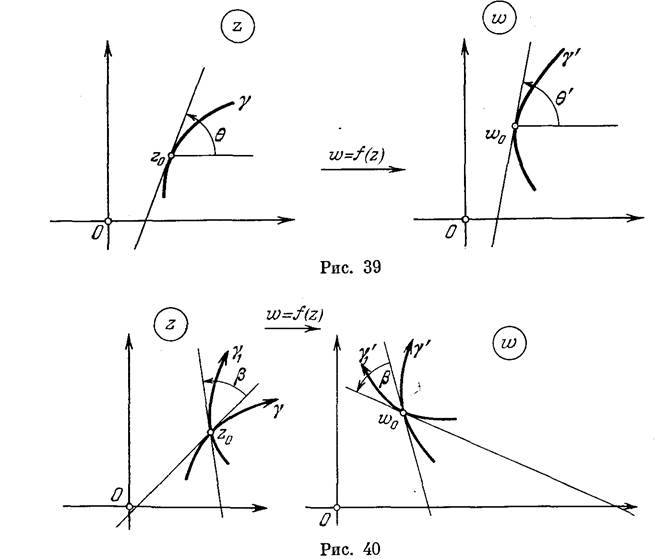
что если /'(zo^O, то угол поворота в точке Zy не зависит от кривой и равен а == arg/'(zo), т. е. все кривые, проходящие через точку Zo, поворачиваются при отображении w=f(z) (/'(zo)'у'5 0) на один и тот же угол, равный аргументу производной в точ­ке г,,.

Таким образом, отображение w==/(z), где /(z)—дифферен­цируемая в окрестности точки Zo функция и /'(Zo^O, сохраняет


74                     ГЛ. II, РЕГУЛЯРНЫЕ ФУНКЦИИ

Из определений 1—2 и свойств производной вытекает, что если функция /(г)

1) дифференцируема в области D,

2) однолистна в области D,

3) ее производная отлична от нуля в этой области, то отображение w=f{z) является конформным.

Заметим, что условие 3) вытекает из условий 1) и 2) (см. §31).

Примеры конформных отображений приведены в п. 2. Линей­ное отображение w = az + b (a ¥= 0) является конформным во всей комплексной плоскости. Далее, функция w = z2 осуществ­ляет конформное отображение верхней полуплоскости Im z > О на плоскость с разрезом [0, +°о). Наконец, отображение w=e' является конформным в полосе 0<1тг<2я.

Более подробно конформные отображения будут изучены в главе VI.

Замечание 2. Если функция регулярна в точке Zo и /'(zo)=0, то отображение iy=/(z) не является конформным в точке Zo. Поясним это утверждение на примере функции /(г)= == z2. В точке Zo=0 производная функции z2 обращается в нуль* (/'(^^Зг). Рассмотрим два луча argz=a и argz=p, выходя­щие из точки z = 0. Их образами при отображении w = z2 явля­ются лучи arg w = 2а и arg w = 2р. Исходные лучи образуют между собой угол Р — а, а их образы—угол 2(^—а). Следова­тельно, углы в точке z=0 удваиваются, т. е. отображение w==z2 не является конформным в точке г == 0.

4. Площадь образа области и длина образа кривой. Пусть функция w=/(z) конформно отображает об­ласть D на область D''. Тогда якобиан отображения равен / =^ == l/^2)!2» и площадь области D' равна

S(D')=\^dudv=^\J\dxdy=\^\f'(z)\•tdxdy.

D'            D                "D

Пусть 7 — кривая, лежащая в областиD, a ^/ — ее образ при отображении w=f{z). Тогда длина кривой ^' равна

;(Y')=Jl^l=J|/'(z)||dz|. т'       т

Замечание 3. Приведем геометрическую интерпретацию формулы (14). Как известно из курса математического анализа, величина |Л, где /—якобиан отображения (13), равняется ко-эффициенту растяжения площадей при отображении (13), т. е. при отображении w =f(z)= u+ iv. Выше было показано, что линейное растяжение при отображении w=f(z) не зависит от направления и равно l/'(Zo)l. Следовательно, коэффициент рас­тяжения площадей равен l/'(zo)12.


§ 9. ИНТЕГРАЛЬНАЯ ТЕОРЕМА КОШИ                75

§ 9. Интегральная теорема Коши

В этом параграфе будет доказана интегральная теорема Коши — один из наиболее важных результатов теории функция комплексного переменного.

1. Теорема Коши для случая непрерывной производной.

Теорема 1. Пусть функция /(z) дифференцируема в одно­связной области D и ее производная непрерывна в D. Тогда ин­теграл от f(z) no любой замкнутой кривой ^, лежащей в области D, равен нулю:

J/ (z)dz=0.(1) •у

Доказательство. Если f{z)==u(x, y)+iu{x, у), то по формуле (3) § 5 имеем

) f(z)dz = /i + iJy ч где

ji = | и dx — v dy, Jg == j v dx + и dy. v                   v

Скачать файл