Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа, страница 18

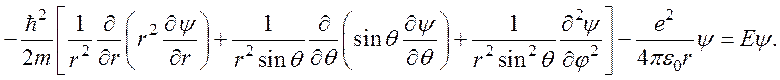
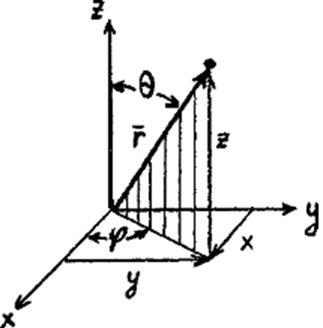
Чтобы решить это уравнение, искомую волновую функцию представляют в виде произведения трех функций, каждая из которых зависит лишь от одной координаты

Функция R, зависящая только от r, называется радиальной. Функция Θ, зависящая только от θ, называется полярной. Функция Ф, зависящая только от φ, называется азимутальной. Оказывается, для функции  можно записать три уравнения, каждое из которых будет содержать только одну из трех функций – R, Θ, Ф. Опустим простые, но достаточно громоздкие преобразования:

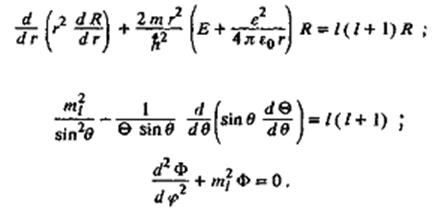
Нетрудно заметить, что в уравнениях появились новые константы l и m_l . Это произошло в процессе разделения исходного уравнения на три.

В комплексной форме решение азимутального уравнения выглядит следующим образом:

       (*)

Так как при повороте системы координат вокруг оси z на угол 2π функция Ф принимает прежнее значение, то должно выполняться условие: m_l= 0, ±1, ±2, ±3,... Таким образом, функции (*) являются собственными функциями азимутального уравнения, а величина m_l является ничем иным, как квантовым числом, определяющим возможные азимутальные функции Ф. Оно называется магнитным квантовым числом.

Перейдем к полярному уравнению. Его решениями являются так называемые присоединенные полиномы Лежандра, которые имеют следующее обозначение: .

Вид полиномов довольно сложен: Для нашего анализа пока важно лишь то, что полиномы зависят от cosθ, и двух параметров – l и m_l . Так как величина m_l может принимать только целые значения (включая ноль), то из общего вида полиномов следует, что величина l может принимать только целые положительные значения (включая ноль), причем должно соблюдаться условие:

Мы получили новое квантовое число l, которое называется орбитальным квантовым числом. Оно совместно с магнитным квантовым числом m_l определяет конкретный вид полярных собственных функций. Из условия  следует, что значение магнитного квантового числа m_l в любом состоянии ограничено величиной орбитального квантового числа l,т.е. m_l=0,±1, ±2,..., ±l.

Это означает, что каждому разрешенному значению l должно соответствовать (2l+1) различных значений m_l. Следовательно, любому фиксированному l соответствует (2l+1) различных полярных собственных функций. Если окажется, что величина энергии состояний при этом одна и та же, то соответствующий энергетический уровень будет иметь (2l+1) – кратное вырождение по m_l.

Осталось рассмотреть уравнение для радиальной функции R. Решение этого уравнения имеет следующий вид:

где  – функции, называемые полиномами Лагерра; l – орбитальное квантовое число; n – любое, отличное от нуля положительное целое число.

В общем виде полиномы Лагерра записываются следующим образом:

Целое число n, определяющее степень полинома и конкретный вид радиальных функций, называется главным квантовым числом. Из вида полиномов Лагерра следует, что должно выполняться соотношение . Следовательно, значение орбитального квантового числа l в состоянии с фиксированным n ограничено величиной n-1.

Таким образом, из решения уравнения Шредингера непосредственно вытекает, что состояние электрона в атоме водорода определяется тремя квантовыми числами:

С учетом этого общее количество возможных состояний (следовательно, и волновых функций) для заданного значения n:

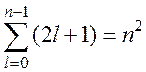
А поскольку у электрона могут быть две ориентации спина (это соответствует двум возможным значениям магнитного спинового квантового числа m_S), общее чисто состояний должно быть равно 2n² . Если окажется, что энергия состояния зависит только от n, то можно будет говорить о 2n² – кратном вырождении энергетических уровней.

Итак, четверка квантовых чисел  полностью определяет состояние электрона в атоме водорода. Основные физические величины, характеризующие состояния, также связаны с этими числами.

Главное квантовое число n определяет энергию состояния:

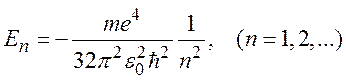
Орбитальное квантовое число l определяет величину орбитального механического момента электрона

Магнитное квантовое число m_l определяет величину проекции орбитального механического момента электрона на выделенное направление z: