Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Режим нагружения сооружения ледяным покровом), страница 6

где d – диаметр опоры.

Таким образом, можно аналитически получить формулы, описывающие процесс взаимодействия опоры со льдом в двух его фазах: внедрение и прорезание. При этом для расчетов нагрузки по формуле (3.23) важно знать скорость льдины и ее площадь, а для случая прорезания (3.35) это не обязательно (учитывая совпадение остальных параметров в обеих формулах).

Но льдина может остановиться и после того, как будет прорезана опорой на расстояние, в несколько раз превышающее размер опоры. В этом случае процесс прорезания будет не стационарным и он не будет описываться ни формулой (3.23), ни формулой (3.35). Для такого случая величины, характеризующие процесс прорезания с постепенным уменьшением скорости льдины и последующей ее остановкой, можно получить проинтегрировав уравнение (3.34):

,                                                                (3.36)

где .

,                                                       (3.37)

Постоянная интегрирования определится из начальных условий:

, , , .

Тогда   ,                                                                                                              (3.38)

Повторное интегрирование (3.38) определит закон изменения глубины прорезания l во времени (С_L=0 из тех же начальных условий):

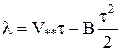,                                                   (3.39)

Время прорезания t_* определится на основании (3.38) с помощью равенства, характеризующего полную остановку льдины (V=0):

,                                                          (3.40

Полное время активного контакта опоры со льдом составит:

,                                                            (3.41)

Для этого случая определение нагрузки на опору следует производить с учетом уменьшения скорости ледяной плиты, иногда приводящее к увеличению предельных разрушающих напряжений на площади F и, соответственно, к увеличению нагрузки. Но с другой стороны, увеличение указанных напряжений за счет уменьшения скорости ледяной плиты лишь ускорит ее остановку.

При полной потери ледяным полем кинетической энергии оно останавливается, а процесс прорезания может возобновиться, когда очередная и последующие дрейфующие льдины соприкоснуться со стоящей у опоры льдиной (случай Г). Согласно данной модели условием возобновления процесса прорезания является превышение силы навала F_s остановившихся перед сооружением ледяных полей, над силой прорезания F_b

,                                                                    (3.42)

Сформулируем теперь основные балансовые соотношения для случая Г, которым подчиняются отдельные компоненты системы «остановившееся ледяное поле - опора МЛП». Пусть x - глубина внедрения. Тогда F_s×x - работа, которую выполняет ледяное поле при его внедрении. Очевиден факт ее расхода на разрушение объема ледяного тела, высота которого равна толщине льда h и площадью основания S, равной площади зоны внедрения опоры в лед (диссипацией внутренней энергии этого тела в силу ее малости можно пренебречь).

В этом случае (Г) работа, которую выполняет ледяное поле при прорезании, равна W=F_sx. Она расходуется на разрушение объема ледяного тела, высота которого равна толщине льда h, а площадь основания S равна площади зоны внедрения опоры в лед. Получаем следующее энергетическое балансовое соотношение

,                                                           (3.43)

где E₀^С - удельная энергия разрушения льда.

Удельная энергия разрушения оценивается по энергии удара, отнесенной к объему разрушенного льда. Численные оценки E₀^С приводятся в [  ]. Левая часть является количественной оценкой работы, которую надо выполнить, чтобы разрушить ледяное тело с площадью основания S и высотой h. В первом приближении зона внедрения представляет собой сектор окружности радиуса r_c. Легко показать, что в этом случае площадь зоны внедрения определяется выражением:

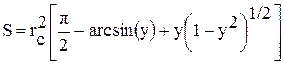,                       (3.44)