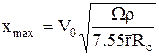Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Режим нагружения сооружения ледяным покровом), страница 5

,                                          (3.22)

Выражение для нагрузки на опору для случая для случая внедрения с остановкой льдины (второй член уравнения (3.30)) получим с учетом (3.33):

,                                      (3.23)

а время до остановки льдины определится из условия

, ,                                            (3.24)

В случае, если энергия ледяной плиты окажется большей , чем требуется на внедрение опоры в лед на глубину x=r, то есть в случае, если будет происходить прорезание ледяного поля опорой (случай Б и В). Из (3.33) можно определить количество энергии, затрачиваемой льдиной или ледовым полем на работу по образованию зоны разрушения льда на глубину x=r. Величина этой энергии, очевидно, должна быть неизменной для льдин и полей льда, имеющих разные толщины, площади и скорость при прочих равных условиях:

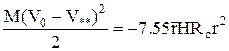,                                    (3.25)

где  и  - начальная скорость льдины и ее скорость в момент времени, соответствующий достижению внедрения в лед на глубину x=r.

Но уравнение (3.25) отражает лишь конечный результат внедрения и не позволяет судить о закономерностях изменения x и V, а соответственно, и нагрузки P в процессе взаимодействия опоры со льдом. В то же время оно дает возможность написать уравнение баланса энергии для процесса внедрения, развивающегося во времени:

                          (3.26)

Здесь V – текущая скорость ледяного поля.

Это уравнение является исходным для выявления указанных закономерностей и характеризует процесс затрат кинетической энергии льдины на нарушение льда в месте ее контакта с опорой. Оно показывает, что для неподвижной опоры скорость изменения кинетической энергии ледяной плиты должна быть равна мощности разрушения льда.

Проведя дифференцирование (3.26), получим:

,                                                (3.27)

Интегрирование (3.27) дает:

,                                     (3.28)

Постоянную интегрирования определим из начальных условий в предположении, что ледовое поле остановилось бы, если имело бы скорость . На самом же деле оно будет продолжать движение, т.к. будет иметь запас кинетической энергии. Скорость V₀₁, погашенную на участке внедрения (0-t_**), можно определить из (3.22), приравняв x_max=r.

Итак, из натурных условий V=V₀₁, x=0 получим:

   и   ,                (3.29)

Интегрирование уравнения (3.29) (С₂=0 при t=0 и x=0) дает закон изменения глубины внедрения опоры в ледяного поле:

,                                                      (3.30)

С учетом (3.30) закон изменения скорости движения льдины перепишется так:

,                                                     (3.31)

Оставшийся запас кинетической энергии ледяного поля, характеризуемый скоростью (V-V₀₁)=V_**, будет расходоваться на прорезание его опорой, которое начнется с момента времени t_**, определяемого как время, затрачиваемое на внедрение опоры на глубину x=r. В этом случае из (3.30) получим:

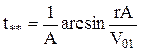.                                               (3.32)

В дальнейшем процесс прорезания опорой ледового поля опишется тем же уравнением (3.26) при условии постоянной площади контакта. Глубина прорезания l теперь будет отсчитываться от x=r так же, как и время прорезания t от t=t_**.

Таким образом,

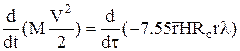 или

                                             (3.33)

где - скорость прорезания.

Но скорость прорезания  является скоростью движения поля в каждый момент времени, поэтому (3.33) можно переписать:

                                          (3.34)

Левая часть этого равенства – сила инерции ледового поля – уравновешивается силой сопротивления льда разрушению, которая описывается выражением в правой части. Уравнение (3.34), с учетом уменьшения расчетной толщины льда согласно [ ], можно представить в виде, принятом на практике расчетов и рекомендуемым СНиПом:

,                                                  (3.35)