Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Режим нагружения сооружения ледяным покровом), страница 14

После математической обработки по программе “Статистика. Планирование эксперимента” получена полиномиальная модель для количества циклов нагружения

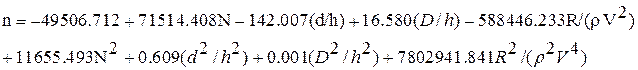 (3.64)

Помимо этого в работе приводится геометрическая интерпретация полученной полиномиальной модели количества циклов нагружения в зависимости от различных сочетаний кодировочных уровней исходных факторов (приложение 1 рис. 3.5 – рис. 3.10).

3.4. Выводы.

Для оценки надежности сооружения с позиций постепенного отказа ( разрушение от накопления усталостных повреждений) необходимо знание вероятностных распределений ледовых нагрузок во всем диапазоне их изменений. Для получения данной информации в работе представлена имитационная модель механического взаимодействия льда с опорой МЛП. На основе этой модели можно определить количество циклов и режим нагружения сооружения ледяным покровом.

Получена полиномиальная зависимость (3.64) количества циклов нагружения n от различных безразмерных комплексов (N, d/h, D/h, R/(rV²)) характеризует влияние входных параметров (скорость дрейфа льда V, толщина ледяных полей h, прочность льда R, диаметр сооружения d, диаметр конструкции D, сплоченность льда N) на величину n может быть использована на предварительных стадиях проектирования МЛП в качестве исходной величины эксплуатационной нагруженности при расчете сооружения на усталостную прочность.