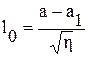Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Режим нагружения сооружения ледяным покровом), страница 4

,                                                (3.13)

Путем использования ранее приведенных выражений и математических преобразований, получим:

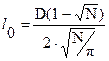,                                           (3.14)

                                                                                                 

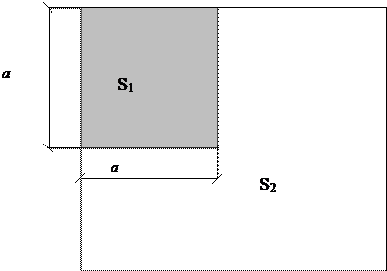
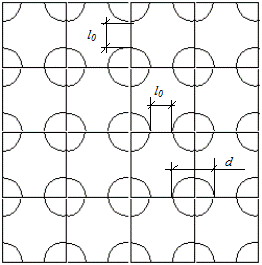
Рис. 3.1                              Рис. 3.2  Схема расположения льдин в квадрате

6. При прорезании ледяного поля оно раскалывается, когда длина полосы прорезания

,                                              (3.15)

7. Граница скалывающейся массы льда проходит по прямой перпендикулярной оси движения льда и через переднюю точку конструкции.

8. Разрушение льда в зоне контакта с опорой носит хрупкий характер, происходит скол и раздробление, а нагрузка ото льда носит циклический характер с частотой разрушения льда при постоянной площади контакта, определяемой по формуле [3]:

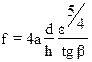,                                                           (3.16)

где а=7¸10 - эмпирический коэффициент, b=45⁰+j/2 - угол скола, j - угол внутреннего трения льда. Схема разрушения ледяной плиты на контакте сооружением приведена на рис. 2.1.

9. Период нагружения (изменение ледовой нагрузки) обратно пропорционален частоте разрушения и определяется по формуле:

,                                                        (3.17)

11. Предполагается, что до опоры гидротехнического сооружения льдины следуют одна за другой на одинаковом расстоянии l₀ между собой. Если перед опорой уже имеются льдины, то расстояние l(t) между крайней льдиной затора и вновь приближающейся льдиной определяется выражением

,                                                 (3.18)

где T - время окончания процесса прорезания и l(0)=l₀.

Для описания механизмов формирования воздействия ледяного покрова, состоящего из отдельных льдин, использовался дискретный подход. При взаимодействии сооружения с ледяной плитой наблюдается четыре характерных случая взаимодействия (см. рис. 3.3).

А) Внедрение опоры сооружения в ледяную плиту (на величину до d/2) и остановка льдины.

Б) тоже, с прорезанием ледяного поля опорой сооружения на величину более d/2 и остановка ледяного поля.

В) тоже, с прорезанием ледяного поля и его раскалывания.

Г) вторичное внедрение или прорезание остановившегося ледяного поля при взаимодействии с проходящими к сооружению другими полями льда.

Для этого используется упрощенные энергетические балансовые соотношения, которые справедливы только для удара плиты о сооружение, что характерно для случаев А, Б, В. Поэтому в первых трех случаях (А, Б, В) рассматривается центральный полностью неупругий удар, когда вся кинетическая энергия приравнивается к работе контактной силы F на пути внедрения опоры x в лед.

Дифференциальное уравнение движения льдины при контакте ее с опорой:

,                                                (3.19)

где М – масса льдины; F- площадь поверхности, на которой происходит смятие льда; x-глубина внедрения опоры в лед; R_c-сила сопротивления разрушающегося от смятия льда, приходящаяся на единицу поверхности.

Аналитически решение данного уравнения можно получить, если зависимость F от x будет линейной. Для случая цилиндрической опоры и с учетом объема смятого льда перед ней эта зависимость приближенно может быть выражена линейно [  ]:

,                                                         (3.20)

где - безразмерный радиус опоры, выражаемый отношением радиуса расчетной опоры к r=1м.

Небольшое отклонение приведенной зависимости от точной можно не принимать во внимание, так как она имеет ощутимую погрешность лишь до значений x<0.25r. Поэтому используем (3.20) для определения нагрузки как на стадии прорезания, так и на стадии внедрения.

Решение уравнения (3.19) с учетом (3.20) запишется так:

,                                                        (3.21)

где .

Максимальная глубина внедрения до остановки льдины перепишется в виде: