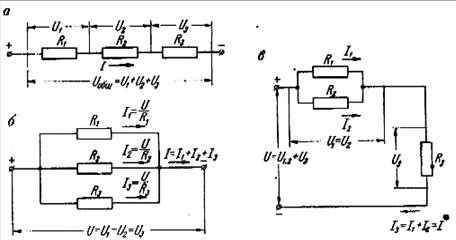
Рис. 7. Способы соединения потребителей.
Через резисторы, включённые последовательно, всегда протекает один и тот же ток.
I1 = I2 = I3 = I.
Этот ток создаёт на каждом из резисторов падения напряжения, пропорциональные их сопротивлениям,
U1 = I∙R1; U2 = I∙R2; U = I∙R3.
Общее напряжение на цепочке из последовательно включённых резисторов равно сумме падений напряжений на отдельных участках
Uобщ = U1 + U2 + U3 = I (R1 + R2 + R3).
При параллельном соединении резисторов (рис. 7, б) общее сопротивление участка уменьшается (так же, как уменьшается сопротивление проводника при увеличении его поперечного сечения).
Общий ток, проходя через параллельно соединённые резисторы, разветвляется в точке их соединения. Проводимость участка с параллельными ветвями увеличивается по сравнению с проводимостью каждого резистора в отдельности и равна сумме проводимостей отдельных ветвей.
gобщ = g1 + g2 + g3.
Так как g = 1/ R, можно написать
1/Rобщ = 1/ R1 + 1/ R2 + 1/ R3.
Напряжение на всех параллельных ветвях одинаково; токи в ветвях зависят от сопротивлений этих ветвей:
I1 = U / R1; I2 = U / R2; I3 = U / R3 .
Из этих формул видно, что токи в ветвях распределяются обратно пропорционально сопротивлениям ветвей:
I1 / I2 = R2 / R1; I2 / I3 = R3 / R2; I1 / I3 = R3 / R1.
В любом разветвлении электрической цепи ток, приходящий к месту разветвления, всегда равен сумме токов, уходящих от разветвления по другим проводникам, т. е.
I = I1 + I2 + I3.
Это правило исходит из невозможности накопления электрических зарядов в точке разветвления проводников и носит название первого закона Кирхгофа.
При смешанном соединении резисторов, показанном на рис. 7, в, ток разветвляется в параллельных ветвях с резисторами R1 и R2 и целиком проходит через резистор R3, включённый последовательно. Общее напряжение на концах такой цепи равно сумме напряжений на параллельном участке и на резисторе, включённом последовательно.
Пример 1. Рассчитать общее сопротивление и падение напряжения в цепи на рис. 8 в, при условии, что I =1 А; R1 = 10 Ом; R2 = 2,5 Ом; R3 = 5 Ом.
Решение. Проводимость параллельных ветвей с сопротивлением R1 и R2
gпар = 1/R1 + 1/R2 = 1/10 + 1/ 2,5 = 0,5 См.
Сопротивление параллельных ветвей Rпар
Rпар = 1/gпар = 1/0,5 = 2 Ом.
Падение напряжения на параллельных резисторах R1 и R2
Uпар = IRпар = 1 · 2 = 2 В.
Токи в резисторах R1 и R2
I1 = Uпар / R1 = 2/10 = 0,2 А;
I2 = Uпар / R2 = 2/2,5 = 0,8 А.
Общее сопротивление смешанной цепи
Rобщ = Rпар + R3 = 2 + 5 = 7 Ом.
Падение напряжения на всей цепи
Uобщ = IRобщ = 1 · 7 = 7 В.
При расчёте сложных разветвлённых цепей, содержащих несколько источников э. д. с., пользуются вторым законом Кирхгофа.
В любом замкнутом контуре цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений в отдельных сопротивлениях:
Σ = Σ Ι∙r
[Буквой Σ (сигма) обозначается сумма].
При этом положительными считаются ЭДС и
падение напряжения, направления которых совпадают с произвольно выбранными
направлениями соответственно обхода контура и тока. Если в результате расчёта ток
получается положительным, это означает, что направление его принято правильным;
в противном случае направление тока будет обратным принятому. Поясним это на
конкретном примере расчёта электрической цепи, содержащей несколько источников
ЭДС.
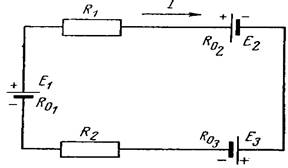
Рис. 8. Схема цепи к расчёту по второму закону Кирхгофа.
Пример 2. Определить величину и направление тока в замкнутой электрической цепи (рис. 8.), если Е1 =6 В;
Е2 = 7 В; Е3 = 4 В; R01 = 0,3 Ом; R02 = 0,5 Ом; R03 = 0,2 Ом; R1 = 7 Ом; R2 = 12 Ом.
Решение. Примем направление обхода контура и тока в нём по часовой стрелке и составим уравнение по второму закону Кирхгофа
Е1 – Е2 – Е3 = IR01 + IR1 + IR02 + IR03 + IR2.
Решим это уравнение относительно тока, подставив значения всех э. д. с. и сопротивлений
I =(E1 – E2 – E3) / (R01 + R1 + R02 + R03 + R2 ) = (6 – 7 – 4)/(0,3+7+0,5+0,2+12)= - 0,25 А.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.