Методические указания к выполнению курсовых работ по дисциплине «Статистика», страница 12

1. Определяем базисный и цепной абсолютный прирост  ()

Базисные:                                                 Цепные:

                      

                       

                       

и т. д.

2. Определяем базисные и цепные темпы роста (Тр)

Базисные:                                                 Цепные:         :

              

              

              

и т. д.

3. Определяем базисные и  цепные  темпы прироста  (Тпр)

Базисные:                                                    Цепные:  

              

               

              

и т. д.

4. Определяем абсолютное значение 1% прироста (А)

                и т.д.

Как показывает таблица 11, наибольшее увеличение себестоимости 1 ц молока с базисным (2001) годом произошло в 2006 и 2004 гг. и составило 306,7 руб. ( 95,7 %) и 183,3 руб. (57,2 %) соответственно. В 2006 году по сравнению с 2005 годом наблюдалось самое заметное увеличение себестоимости продукции – на 151,6 руб. (31,9 %), а наибольшее снижение за 2004-2005 гг. – на 28,2 руб. (5,6 %).

Для обобщающей характеристики динамики исследуемого показателя определяются средние показатели.

Средний уровень ряда () показывает среднее значение уровня ряда за анализируемый период и рассчитывается по формуле:

      ( 17 )

где n – число уровней ряда (лет).

 руб.

Средний абсолютный прирост показывает скорость изменения показателя и рассчитывается по формуле:

      ( 18 )

где n - число уровней ряда динамики;

 - первый (базовый) уровень ряда динамики;

- последний уровень ряда динамики;

 - цепные абсолютные приросты.

 61,3 руб.

Средний темп роста  можно определить, пользуясь формулой:

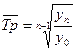*100      ( 19 )

 111,8 %

Средний темп прироста  :

      ( 20 )

 

Следовательно, за 2001-2006 гг.  средняя себестоимость 1 ц молока составила 443,1 рубля. За каждый год данного периода себестоимость возрастала на 61,3 рубля или на 11,8 %.

В дальнейшем необходимо выявить тенденцию развития показателя в динамике. Для этой цели применяют метод аналитического выравнивания. Он является наиболее совершенным методом выявления тенденции ряда динамики и заключается в замене первоначальных уровней ряда новыми, найденными во времени "t" построением аналитического уравнения связи.

Рассмотрим на примере данные таблицы 12 возможности применения аналитического метода выравнивания для выявлении тенденции ряда динамики (себестоимости 1 ц молока) и его прогнозировании.

Вначале расставляют порядковый номер года в ряду динамики (графа t) - от 1 до 6, вносят исходные данные по ряду динамики (графа y). Далее рассчитывают значения по каждому уровню ряда: t², yt, а также суммы по графам: Σt, Σy, Σt², Σytи вносят их в таблицу.

Таблица 12

Выравнивание и прогнозирование динамического ряда

себестоимости 1 ц молока

Годы	Порядковый номер года	Себестоимость 1 ц молока,  руб.	Расчетные данные		Выровненный ряд
	t	y	t2	yt	yt = a + b∙t
2001	1	320,5	1	320,5	301,0
2002	2	375,6	4	751,2	357,8
2003	3	355,8	9	1067,4	414,7
2004	4	503,8	16	2015,2	471,5
2005	5	475,6	25	2378	528,3
2006	6	627,2	36	3763,2	585,2
	Σt = 21	Σy = 2658,5	Σt2 = 91	Σyt = 10295,5	Σyt = 2658,5

Судя по тенденции себестоимости 1 ц молока за 2001-2006 гг., можно сказать, что наиболее вероятна линейная зависимость данного распределения от времени "t" и данному распределению соответствует уравнение прямой: