Методические указания к выполнению курсовых работ по дисциплине «Статистика», страница 10

Для определения коэффициента регрессии можно использовать уравнение прямой:

      ( 7 )

Параметры уравнения а и b находят, решая систему линейных уравнений:

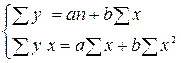     ( 8 )

Подставляя данные таблицы, получаем:

Решаем систему уравнений:

Из второго уравнения вычитается первое уравнение, в результате чего параметры «а» сокращаются:

Теперь определим параметр «а», подставив в первое уравнение найденное значение «b»:

Следовательно, уравнение регрессионной модели себестоимости  1 ц молока примет вид:

Y_х = 143,65 + 23,82∙х

Коэффициент регрессии при х показывает, как в среднем по совокупности районов изменяется результативный показатель при увеличении факторного на единицу его измерения.

Таким, образом, при увеличении трудоемкости производства 1 ц молока на 1 чел. час. себестоимость производства 1 ц молока по совокупности районов вырастет на 23,82 рублей.

В четвертом разделе курсовой работы проводится индексный анализ показателя (трудоемкости, себестоимости, прибыли от реализации продукции).

Для индексного анализа выбирают два района из совокупности (раздел 1), как правило, с наименьшим и наибольшим значением показателя. Затем все исходные данные заносят в таблицу,используядля этого базу данных, приведенную в приложениях 1-3, а также рассчитывают необходимые для индексного анализа показатели.

В качестве сравниваемой величины (числитель индексного отношения) выбирают район с наибольшим значением показателя. Величину, с которой проводится сравнение (база сравнения), служит район с наименьшим значением показателя.

При проведении индексного анализа показатели сравниваемой величины обозначают с индексом «1» (Z₁ , Y1, T1, t₁, q₁, p₁), а базы сравнения - с индексом «0» (Z₀ , Y₀, T₀, t₀, q₀, p₀.). Используя формулы, определяют общее изменение показателя в относительном и абсолютном выражении, а также влияние на его увеличение или уменьшение других факторов. Выполняют проверку полученных расчетов и делают выводы.

В качестве примера рассмотрим  индексный анализ себестоимости 1 ц молока.

Ранее установили, что из 18 районов области (раздел 1) наименьшее и наибольшее значение себестоимости 1 ц молока имеют Новозыбковский и Клетнянский районы – 0,30 и 0,55 тыс. руб. соответственно. Эти данные, а также среднегодовое поголовье коров, затраты на производство и количество молока из базы данных записывают в таблицу 10 .

Рассчитывают затраты на 1 голову и продуктивность скота, используя формулы в приложениях по теме курсовой работы «Экономико-статистический анализ себестоимости молока».

    (9)

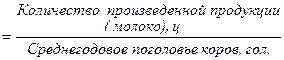     (10)

Таблица 10

Исходные данные для индексного анализа себестоимости 1 ц молока

Показатели	Символы	Наименование района	Наименование района
		Новозыбковский	Клетнянский
Среднегодовое поголовье, гол.		5000	1368
Затраты на производство, тыс. руб.		32527	9529
Количество произведенной продукции, ц		108645	17339
Затраты на 1 голову, тыс. руб.	YZ	6,51	6,97
Надой молока на 1 корову, ц	Y	21,73	12,67
Себестоимость 1 ц, тыс. руб.	Z	0,30	0,55

В качестве сравниваемой величины выбираем район с наибольшим значением себестоимости 1 ц молока – Клетнянский. Величину, с которой проводится сравнение (база сравнения), служит район с наименьшим значением показателя – Новозыбковский.

Общее изменение себестоимости 1ц продукции:

 (183,3 %)

Абсолютное отклонение себестоимости 1 ц продукции:

 тыс. руб.

Изменение себестоимости 1 ц продукции:

а) вследствие изменения затрат на 1 голову:

 (107,0%)

абсолютное изменение себестоимости 1ц продукции за счет изменения затрат на 1голову:

 тыс. руб.