Такие элементы как кислород, азот и водород неминуемо попадают в жидкую сталь вследствие контакта металла с окружающей атмосферой. Данные раздел посвящён расчётным оценкам поведения азота и водорода в жидкой стали. Кислород и его удаление будут рассмотрены в следующей части. В большинстве случаев растворённые в металле азот и водород резко снижают качество стали. Из жидкого металла растворённые газы могут быть удалены посредством вакуумирования, экстракции пузырями СО в процессе окисления углерода, при продувке инертными газами. Для контроля содержания газов необходимо уметь рассчитывать их растворимость в жидкой стали (стандартную и равновесную с атмосферой заданного состава) и изменения содержаний под влияние различных условий (вакуумирование, окислительная продувка, введение легирующих компонентов).
Домашнее задание № 3
Исходные данные – температура жидкой стали и её состав, начальные содержания азота и водорода, величина понижения температуры, остаточное давление в вакуумной камере и содержание титана – приведены в приложении В. Для выполнения домашнего задания по теме «Газы в жидкой стали» требуется:
1) Построить зависимости конечных содержаний азота и водорода от количества окисленного углерода в интервале значений ∆С от 0 до 1%. Начальные содержания газов: [N]нач и [H]нач. Поступлением азота и водорода из газовой фазы и материалов пренебречь. Определить количество углерода (%), которое необходимо окислить для получения конечных содержаний газов на уровне [N]=0,004% и [H]=0,0002%.
2) Определить равновесные с газовой фазой содержания азота и водорода в готовой жидкой стали в ковше-печи при заданных температуре и составе газовой фазы. Определить количество азота и водорода (в %, в ppm и в см3/100 г.), которое может выделиться из жидкой стали при понижении температуры на ∆t °С.
3) Определить равновесные содержания азота и водорода, а также максимальную степень дегазации (%) жидкой стали при вакуумировании. Остаточное давление в вакуумной камере – Pост.
4) Определить возможность образования нитридов титана в жидкой стали при заданном содержании титана. Оценить термодинамическую температуру, при которой начинают образовываться нитриды.
Решение варианта № 0.
Растворённые в жидком полупродукте газы (азот и водород) могут быть удалены при проведении окислительного рафинирования. При продувке кислородом углерод окисляется до СО. При этом образовывающиеся в объеме жидкого металла пузырьки СО для растворённых газов могут выступать в качестве «химического» вакуума, так как парциальное давление растворённых газов в пузырьке пренебрежимо мало. Вследствие того, что парциальное давление газов в объеме металла выше, чем в пузырьках СО, азот и водород переходят из расплава в пузырьки СО. Рассчитаем минимальное содержание газов, которое можно получить при дегазации по механизму удаления газов в пузырьках СО.
Рассмотрим парциальное давление двухатомного газа (N2 или H2) в пузырьке СО
,
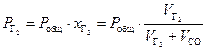(3.1)
где 
– мольная доля газа Г2
в пузырьке СО;
, 
– объёмы газов Г2
и СО в пузырьке.
Объём выделившегося газа связан с концентрацией в жидкой стали соотношением
,
(3.2)
где ∆[Г] – количество выделившегося газа при окислительном рафинировании, %;
mMe – масса металла, г;
Vm – объём одного моля газа при температуре окружающей среды (для нормальных условий Vm = 22,4 л/моль), л/моль;
– молярная масса молекулы Г2,
г/моль.
Аналогично для объёма образующегося оксида углерода при продувке жидкого металла кислородом
,
(3.3)
где ∆С – количество окисленного за время продувки углерода, %;
– молярная масса углерода, г/моль.
Подставляя (3.2) и (3.3) в (3.1) получаем
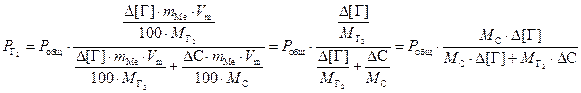. (3.4)
Парциальное давление газа связано с его концентрацией через константу равновесия
.
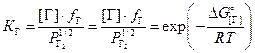
(3.5)
Для растворов азота и водорода в жидком железе справедливы соотношения fN = 1 и fH = 1. Подставляя (3.5) в (3.4) получаем
.
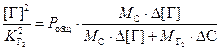Проведём преобразование полученного выражения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.