Первое уравнение в системе (1.6) – это уравнение материального баланса фосфора в системе «металл–шлак». Второе уравнение – это выражение коэффициента распределения фосфора между металлом и шлаком.
Выразим конечное
содержание фосфора в шлаке из второго уравнения системы 
и
подставим в первое:
.
Разделим обе части
уравнения на массу металла mМе
и введём кратность шлака 
.
Отсюда конечное содержание фосфора в металле
. (1.17)
В условиях домашнего задания начальное содержание фосфора в шлаке (Р)Н = 0, тогда
. (1.18)
Отметим, что в реальных условиях начальное содержание фосфора в шлаке никогда не равно нулю. Степень дефосфорации будет равна
.
(1.19)
Рассчитаем
конечное содержание фосфора для варианта № 0
(
) при кратности шлака 5%.
При этом необходимо помнить, что в расчетных уравнениях (1.18) и (1.19)
кратность шлака надо подставлять в долях, то есть λ = 0,05:
.
При этом степень дефосфорации:
.
При кратности шлака 10% (λ = 0,1) конечное содержание фосфора:
.
При этом степень дефосфорации:
.
Расчет показывает, что при увеличении количества шлака (кратности λ) конечное содержание фосфора в жидкой стали снижается, а степень дефосфорации увеличивается.
Минимальное количество шлака (кратность λ), необходимое для получения заданного конечного содержания фосфора в жидкой стали, можно выразить из уравнения (1.18)
.
(1.20)
Для варианта № 0 необходимо снизить содержание фосфора в 10 раз ([P]Н = 0,05%, [P]K = 0,005%):
.
Для получения 0,005% фосфора в жидком полупродукте необходимо иметь шлак заданного состава в количестве 8,44% от массы металла, например, для 100 тонн стали требуется 8,44 т. жидкого шлака.
Коэффициент
распределения фосфора зависит от температуры. Эту зависимость для шлака состава
варианта № 0 можно получить из
уравнения (1.15), приняв, что состав от температуры не зависит. Заменив в (1.15)
активность FeO на 
и коэффициент активности
катиона фосфора на 
,
получаем
. (1.21)
Зависимость коэффициента активности фосфора в металле от температуры можно вычислить в приближении теории регулярных растворов:
.
Постоянная и независящая от температуры для данного состава шлака величина в выражении (1.21) равна
.
Зависимость коэффициента активности катиона железа в шлаке от температуры по модели РИР для шлака заданного состава
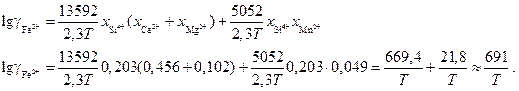
Подставляем полученные выражения в (1.21)
.
На рисунке 1.1 представлена зависимость коэффициента распределения фосфора от температуры для состава шлака варианта № 0.
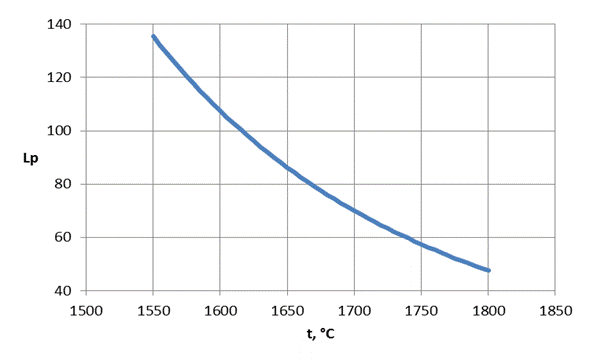
Рисунок 1.1 – Зависимость коэффициента распределения фосфора от температуры
Как видно из графика, с повышением температуры коэффициент распределения фосфора между металлом и шлаком уменьшается, степень дефосфорации снижается. Таким образом, повышение температуры отрицательно влияет на процесс дефосфорации.
Коэффициент
распределения фосфора также зависит от окисленности системы (активности оксида
железа). В грубом предположении, что состав шлака с изменением активности FeO остается неизменным и 
, Ʃni
не зависят от состава, при 1600 °С
по уравнению (1.15) получаем
.
На рисунке 1.2 представлена зависимость коэффициента распределения фосфора от активности FeO для состава шлака варианта № 0.
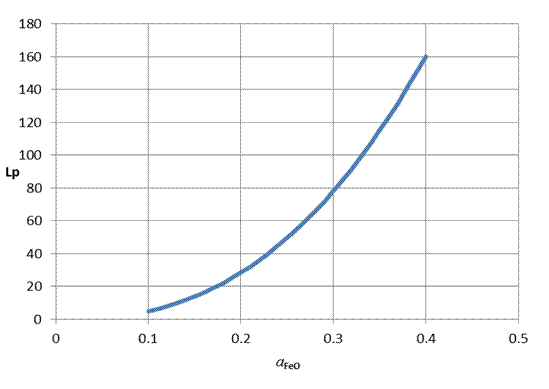
Рисунок 1.2 – Зависимость коэффициента распределения фосфора от активности FeO
Как видно из графика, с ростом активности оксида железа коэффициент распределения фосфора между металлом и шлаком увеличивается, степень дефосфорации повышается. Таким образом, повышение окисленности системы положительно влияет на процесс дефосфорации.
Состав стали влияет на процесс дефосфорации путем изменения коэффициента активности фосфора в жидком металле. Изменение коэффициента распределения фосфора при добавлении компонента [R] можно получить из уравнения (1.15)
.
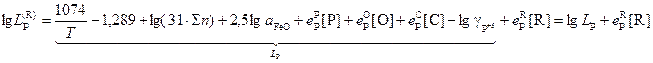
(1.22)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.