Практикум по выполнению домашних заданий по курсу «Современные проблемы металлургии и материаловедения», страница 4

Qij, кДж/моль	FeO	MnO	CaO	MgO	SiO2	Р2О5
FeO	0	0	0	0	0	0
MnO	0	0	0	0	-42	0
CaO	0	0	0	0	-113	-200
MgO	0	0	0	0	-113	0
SiO2	0	-42	-113	-113	0	0
Р2О5	0	0	-200	0	0	0

Состав шлака варианта № 0 (массовая доля, %): FeO – 18, MnO – 6, CaO – 44, MgO – 7, SiO₂ – 21, Al₂O₃ – 4. В.А. Кожеуров не рассматривал оксид алюминия в своих шлаках, но, как правило,  Al₂O₃ в этих системах ведёт себя как нейтральный компонент и можно принять, что его энергии смешения равны нулю со всеми оксидами ().

Для нахождения ионных долей катиона воспользуемся следующими молярными массами оксидов (г/моль): FeO – 72, MnO – 71, CaO – 56, MgO – 40, SiO₂ – 60, Al₂O₃ – 102. Рассчитаем количество молей катионов Ʃn_i в 100 граммах шлака. В дальнейших расчетах, масса шлака сокращается, поэтому удобно использовать 100 грамм шлака, так как в этом случае процентное содержание оксида численно равно его массе:

.

Отношение массовой доли оксида алюминия к его молярной массе необходимо умножить на 2, так как Al₂O₃ содержит два катиона металла. Для нахождения ионной доли катионов разделим количество молей соответствующего катиона n_i на общее число молей всех катионов Ʃn_i:

;

;  .

Ионные доли катионов целесообразно округлять до третьего знака после запятой. Выражение для коэффициента активности катиона железа (1.9) удобно использовать в виде:

.

При температуре 1600 °С (1873 К) для шлака заданного состава получаем

.

Активность FeO в шлаке при 1600 °С

.

Для расчета равновесного кислорода и углерода под шлаком заданного состава необходимо знать константы равновесия. При 1873 К К_FeO = 4,39 и К_C = 114 (см. приложение Е).

Равновесное содержание кислорода под заданным шлаком:

.

Равновесное содержание углерода под заданным шлаком:

.

Содержания элементов целесообразно округлять до тысячных долей процентов.

Процесс дефосфорации под окислительным шлаком описывают реакцией [5]:

.      (1.11)

За стандартное состояние фосфора принят гипотетический однопроцентный раствор фосфора в жидком железе, обладающий свойствами бесконечно разбавленного; для оксида фосфора – чистый жидкий P₂O₅. Константа равновесия реакции (1.11) K_P имеет вид

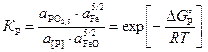,                                         (1.12)

где  – активность оксида РО_2,5 в шлаке;

a_[Р] – активность фосфора в жидком железе.

Примем, что жидкий металл – практически чистое железо, тогда . Подставляя  и  в (1.12) получаем

.                                     (1.13)

Коэффициент распределения фосфора L_P часто используют в виде L_P = (P)/[P], где (P) – массовая доля фосфора в шлаке, %. Ионная доля катиона фосфора в шлаке связана с его массовой долей соотношением , так как . Молярная масса фосфора 31 г/моль, тогда (1.13) примет вид

.                    (1.14)

Выражение (1.14) позволяет по известным составам металла (f_P) и шлака (), и заданной температуре (K_P) рассчитать коэффициент распределения фосфора. Для расчетов выражение (1.14) удобно использовать в логарифмическом виде. Учтём, что  и lgK_P = 1074/T –1,289. Тогда

.                      (1.15)

Коэффициент активности катиона фосфора в шлаке можно найти по уравнению (1.10)

Значения параметров взаимодействия из приложения 5 , начальное содержание фосфора для варианта № 0 [P] = 0,050%.

           

Для определения конечного содержания фосфора в жидком металле составим систему уравнений

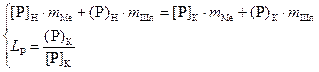 ,                             (1.16)

где m_Me, m_Шл  – массы металла и шлака соответственно;

[P]_H, [P]_K, (P)_H, (P)_K – начальные и конечные содержания фосфора в металле и шлаке, %.