Практикум по выполнению домашних заданий по курсу «Современные проблемы металлургии и материаловедения», страница 10

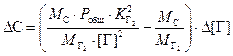
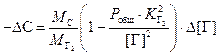.                                  (3.6)

Поскольку при удалении газов парциальное давление , то формулу (3.6) нельзя использовать напрямую для расчета конечной концентрации растворённого газа при окислении заданного количества углерода (∆С). Для получения корректного уравнения необходимо в (3.6) разности ∆С и ∆[Г]  заменить на дифференциалы dС и d[Г], и провести интегрирование уравнения (3.6) от начальных содержаний (С_Н, [Г]_Н) до конечных (С_К, [Г]_К).

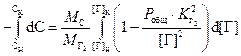
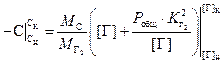
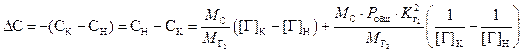.   (3.7)

Расчёты удаления азота и водорода по формуле (3.7) показывают, что вклад слагаемого  не  превышает 2% отн. Поэтому (3.7) удобно переписать в виде

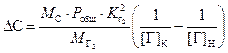.                                   (3.6)

Уравнение (3.6) принято называть формулой Геллера, которая количественно описывает удаление растворённых в жидкой стали газов с пузырьками СО при проведении окислительного рафинирования металла.

Преобразовав (3.6), получаем формулу Геллера для расчета текущей равновесной концентрации азота при обезуглероживании

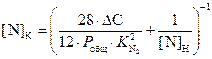.                                      (3.7)

Формула Геллера для расчета текущей равновесной концентрации водорода при обезуглероживании

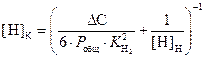.                                      (3.8)

При обезуглероживании в открытой печи можно принять, что Р_общ = 1 атм. Реакция растворения азота в жидком железе имеет вид

.                        (3.9)

Константа равновесия реакции (3.9) (см. приложение Е) при 1600 °С , начальное содержание азота [N]_H = 0,016% для варианта №0. На рисунке 3.1 представлена зависимость содержания азота от количества окисленного углерода при продувке жидкого железоуглеродистого полупродукта кислородом.

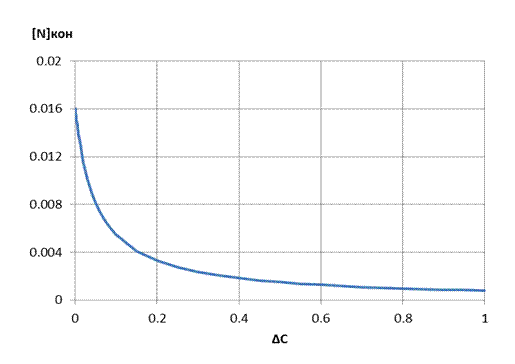
Рисунок 3.1 – Зависимость концентрации азота от количества окисленного углерода

Реакция растворения водорода в жидком железе имеет вид

.                        (3.10)

Для водорода при 1600 °С  (см. приложение Е), начальное содержание [Н]_H = 0,0016% для варианта №0. На рисунке 3.2 представлена зависимость содержания водорода от количества окисленного углерода при продувке жидкого полупродукта кислородом.

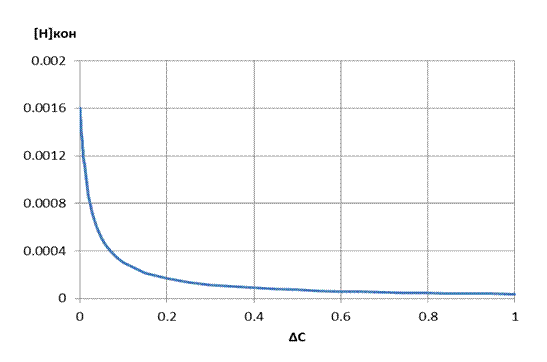
Рисунок 3.2 – Зависимость концентрации водорода от количества окисленного углерода

Для определения количества углерода, необходимого для получения заданного содержания азота ([N]_К = 0,004%), перепишем уравнение (3.6) применительно к удалению азота

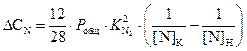.                                     (3.11)

Для варианта №0 .

Для определения количества углерода, необходимого для получения заданного содержания водорода ([Н]_К = 0,0002%), запишем уравнение (3.6) для случая рафинирования расплава от водорода

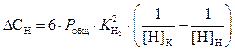.                                      (3.12)

Для варианта №0 .

Равновесное с газовой фазой содержание азота можно рассчитать, рассмотрев выражение для константы равновесия реакции (3.9)

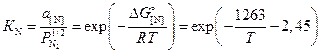.                           (3.13)

С учётом выражения для активности азота a_[N] = [N]·f_N получаем

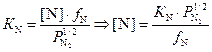.                                             (3.14)

Для заданного состава газовой фазы (N₂ = 78%  об.) парциальное давление азота

.

где  – мольная доля азота в виде N₂ в газовой фазе.

Коэффициент активности азота можно найти по составу жидкой стали с использованием массовых параметров взаимодействия с учётом температурной зависимости, предложенной Чипманом и Корриганом (John Chipman, D.A. Corrigan) и отвечающей модели квазирегулярных растворов:

,                                     (3.15)

где k – число компонентов жидкой стали.

Для состава стали варианта №0 при 1873 К из приложения 5: ,  и .

.

Отсюда равновесное с газовой фазой (N₂ 78% об.) содержание азота в жидкой стали состава варианта №0 по уравнению (3.14)

.

Отметим, что фактические содержания азота в стали ниже полученного значения и составляют обычно от 0,008…0,020%. Это несоответствие вызвано наличие защитного шлакового слоя на поверхности жидкого металла.

Равновесное с газовой фазой содержание водорода можно рассчитать, рассмотрев константу равновесия реакции (3.10)

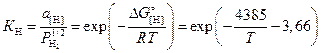.                           (3.16)

С учётом выражения для активности водорода a_[Н] = [Н]·f_Н получаем

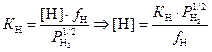.                                             (3.17)