Математические модели и модели экспертизы вагоноремонтного производства

Классификация математических моделей

Математические модели позволяют заменить реальные объекты с некоторой степенью приближения и дают возможность проводить всесторонний  анализ объектов.

Правильный выбор математической модели зависит от понимания задачи, цели действий и критерия эффективности. Руководитель, использующий результаты исследований, должен знать и понимать, какая была применена математическая модель, какие факторы ею учтены, какие факторы остались вне расчетов, и следовательно подлежат качественной оценке.

Применяемые для исследования производственных процессов математические модели можно классифицировать по трем признакам [1;3]:

1. Целевому назначению (экономико-математические, модели операций);

2. Методу решения (аналитические, численные, статистические, комбинированные, математического программирования);

3. Характеру исследуемых величин (детерминированные, стохастические).

Экономико-математические модели связывают факторы, часть которых имеют экономический смысл (модель себестоимости, модель приведенных затрат и др.). Модели операций описывают процессы функционирования системы при реализации каких-либо ее функций: надежности, динамики, производительности, устойчивости и др.

Аналитические модели представляют собой алгебраические уравнения в виде известных функций. Они могут учитывать небольшое число факторов, требуют допущений и упрощений. Но зато они наглядны и отчетливее отражают присущие объекту закономерности. Они наиболее приспособлены для поиска оптимальных решений.

Численные модели сводятся к арифметическим и логическим действиям над числами при наличии ограничений. Численные модели, по сравнению с аналитическими, более точны и подробны, не требуют грубых допущений, позволяют учесть большее число факторов, ближе к действительности. Но они громоздки, требуют значительного расхода машинного времени, имеют плохую обозримость полученных результатов, требуют применения вычислительных методов и ЭВМ.

Комбинированные или  аналитико-численные  модели позволяют по аналитическим зависимостям устанавливать общие закономерности протекания процесса, а по численной – уточнять результаты.

Статистические модели предназначены для обработки статистических данных, полученных в результате наблюдений или численных экспериментов.

Модели линейного математического программирования решают задачи оптимизации производственных или транспортных систем.

Статистические модели и модели линейного математического программирования наиболее широко применяются для исследования производственных процессов и систем.

При построении статистических моделей применяют методы корреляционного и регрессионного анализа, метод Монте-Карло (метод статистического моделирования). Метод Монте-Карло  – построение искусственного случайного процесса, обладающего всеми нужными свойствами и реализуемого с помощью обычных вычислительных средств. Метод Монте-Карло для приближенного нахождения численных значений какой-либо величины  заключается в кратной выборке значений случайной величины  в серии независимых испытаний и вычислении среднего значения .

Тогда по закону больших чисел при достаточно большом значении  с вероятностью, достаточно близкой к единице,

.

С помощью этого метода можно установить частоту появления неисправностей, фактические размеры дефектов и решить многие другие задачи.

К моделям линейного математического программирования относят математические модели, в которых единственная целевая функция и ограничения заданы аналитически. Целевая функция должна представлять собой линейную зависимость от переменных, а ограничения могут представлять собой систему равенств и неравенств.

Основная задача линейного программирования состоит в выборе  из всех неотрицательных решений заданной системы линейных алгебраических уравнений такого решения, при котором целевая функция принимает наименьшее или наибольшее значение.  Для сведения прикладных задач к основной задаче линейного программирования необходимо:

·  Определить целевую функцию;

·  Сформулировать ограничения;

·  Выбрать метод решения системы уравнений.

Применение метода статистического моделирования

для определения частоты появления неисправностей

Постановка задачи: определить  частоты  появления неисправностей у боковых рам тележек грузовых вагонов в эксплуатации (статистическая математическая модель).

В эксплуатации у боковых рам тележек грузовых вагонов могут появляться дефекты, обозначенные на рис 6.

Требуется определить частоту появления обозначенных неисправностей в эксплуатации. Полагаем, что частота появления неисправностей имеет нормальный закон распределения с параметрами: среднее значение 0,5; стандартное отклонение 0,1.

3

2

1

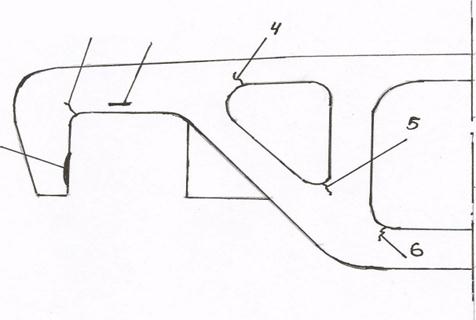
Рис. 6. Основные неисправности боковых рам:

1 – износ поверхности направляющей букс;

2,3,4,5,6 – трещины

Будем полагать, что  шаг изменения случайной величины: .

Поскольку неисправностей шесть, то для изменения случайной величины сформируем шесть интервалов:

1.  0 - 0,1666;

2.  0,1666 - 0,3332;

3.  0,3332 - 0,4998;

4.  0,4998 – 0,6664;

5.  0,6664 – 0,8330;

6.  0,8330 – 0,9996.

Связываем искусственный процесс генерирования случайных величин с реальным – неисправностями боковой рамы. Первую неисправность отождествляем с первым интервалом и т.д. (порядок – произвольный, но должен быть определен до «розыгрыша»).

Разработка программы автоматизации решения задачи.

Технология генерации случайных чисел.

·  Входим в Excel

·  Сервис-Анализ данных - Генерирование случайных чисел - ОК.

·  Вводим  необходимые данные:

Число переменных (указывается число столбцов в таблице, в нашем случае 1);

Число случайных чисел (число строк в столбце, например, 50, 100, 1000 и др., принимаем для рассматриваемого примера - 50);

Распределение – нормальное.

Параметры:

Среднее значение – 0,5;

Стандартное отклонение -  0,1

Случайное рассеивание – 0 (можно не указывать)

Выходной интервал – А1:А50, ОК

Формирование интервалов:

·  В ячейке B1 записываем 6;

·  В ячейке B2 размещаем формулу = 1/B1;

·  В ячейке В3 записываем формулу = B2+$B$2;

·  Копируем эту формулу в ячейки В4-В7, получая в них интервалы значений случайной величины;

Определение количества попаданий случайной величины:

·  В столбце С выделяем ячейки С1:С6;

·  Вызываем функцию - категория статистические – Частота – ОК;

·  Массив данных А1:А50

·  Массив интервалов В2:В7

·  Указатель  мыши подводим в строке формул к знаку =(знаку функции ) и щелкаем ЛКМ;

·  Нажимаем Ctrl+Shift+Enter (признак матричной операции) и получаем в ячейках С1:С6 – число попаданий случайной величины в интервалы;

·  В ячейке С7 набираем формулу =СУММ(С1:С6). Должно получиться фактическое число попаданий.