Определение частоты попаданий – вероятностей появления неисправностей:
· В ячейке D1 набираем формулу = С1/$C$7;
· Копируем эту формулу в другие ячейки (D2-D6), получая в них значения частот;
· В ячейке D7 набираем формулу = СУММ(D1:D6). Должна получиться «1»;
· Номер каждой ячейки соответствует вероятности появления неисправностей: 1- 0,015; 2 – 0,122; 3 – 0,353; 4 – 0,379; 5 – 0,117; 6 – 0,014.
Модели линейного программирования
К моделям линейного программирования относят математические модели, в которых единственная целевая функция и ограничения заданы аналитически. Основная задача линейного программирования состоит в определении из всех неотрицательных решений заданной системы линейных алгебраических уравнений такое, при котором целевая функция принимает наименьшее или наибольшее значение. Как правило, целевая функция представляет собой сумму расходов или прибыль. Экстремальные значения функций в задачах линейного программирования достигаются всегда в точках, где производная не существует. Тем самым при решении таких задач методы дифференциального исчисления не применимы.
Для решения задач линейного программирования можно применить интегрированный пакет Microsoft Office/ Microsoft Excel.
Распределение потребных мощностей деповского ремонта вагонов по железным дорогам
Целевая функция, выражающая общие затраты на деповской ремонт вагонов,
записывается так: 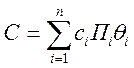 ,
,
где ![]() себестоимость деповского ремонта
одного приведенного вагона на i- ой железной дороге;
себестоимость деповского ремонта
одного приведенного вагона на i- ой железной дороге;
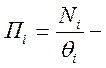 средний съем вагонов с одной
ремонтной позиции достигнутый на i- ой железной дороге;
средний съем вагонов с одной
ремонтной позиции достигнутый на i- ой железной дороге;
![]() годовой объем выпуска вагонов на i- ой
железной дороге;
годовой объем выпуска вагонов на i- ой
железной дороге;
![]() количество ремонтных позиций,
имеющихся на i- ой железной дороге.
количество ремонтных позиций,
имеющихся на i- ой железной дороге.
В качестве ограничений принимаются следующие условия:
![]() Целое;
Целое; ![]()
![]() Здесь
Здесь ![]() доля
участия i- ой железной дороги в деповском ремонте вагонов
(статистические данные); ПВ – общая годовая потребность грузовых вагонов в
деповском ремонте.
доля
участия i- ой железной дороги в деповском ремонте вагонов
(статистические данные); ПВ – общая годовая потребность грузовых вагонов в
деповском ремонте.
Входим в Excel.
· Вводим исходные данные и формулы в ячейки А1:I18 (данные условные, см. табл.7):
Таблица 7
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
|
|
1 |
Дорога |
Пi |
|
ci |
|
ПВ |
|
|
|
|
2 |
ОКТ |
523 |
0,092 |
3100 |
104 |
400000 |
=B2*E2 |
=C2*F2 |
=D2*G2 |
|
3 |
Моск |
513 |
0,089 |
3040 |
125 |
=F2 |
=B3*E3 |
=C3*F3 |
=D3*G3 |
|
4 |
Горьк |
594 |
0,048 |
5140 |
69 |
=F2 |
=B4*E4 |
=C4*F4 |
=D4*G4 |
|
5 |
Сев |
522 |
0,068 |
4304 |
78 |
=F2 |
=B5*E5 |
=C5*F5 |
=D5*G5 |
|
6 |
С-Кав |
543 |
0,088 |
3200 |
97 |
=F2 |
=B6*E6 |
=C6*F6 |
=D6*G6 |
|
7 |
Юго-В |
493 |
0,034 |
4400 |
71 |
=F2 |
=B7*E7 |
=C7*F7 |
=D7*G7 |
|
8 |
Прив |
546 |
0,031 |
4600 |
68 |
=F2 |
=B8*E8 |
=C8*F8 |
=D8*G8 |
|
9 |
Куйб |
602 |
0,058 |
4320 |
79 |
=F2 |
=B9*E9 |
=C9*F9 |
=D9*G9 |
|
10 |
Свердл |
604 |
0,111 |
4306 |
83 |
=F2 |
=B10*E10 |
=C10*F10 |
=D10*G10 |
|
11 |
Южно-У |
633 |
0,072 |
4200 |
82 |
=F2 |
=B11*E11 |
=C11*F11 |
=D11*G11 |
|
12 |
Зап-Сиб |
559 |
0,029 |
5400 |
69 |
=F2 |
=B12*E12 |
=C12*F12 |
=D12*G12 |
|
13 |
Кем |
610 |
0,107 |
5600 |
41 |
=F2 |
=B13*E13 |
=C13*F13 |
=D13*G13 |
|
14 |
Красн |
615 |
0,058 |
6100 |
19 |
=F2 |
=B14*E14 |
=C14*F14 |
=D14*G14 |
|
15 |
В -Сиб |
538 |
0,054 |
4700 |
67 |
=F2 |
=B15*E15 |
=C15*F15 |
=D15*G15 |
|
16 |
Забайк |
462 |
0,019 |
5000 |
58 |
=F2 |
=B16*E16 |
=C16*F16 |
=D16*G16 |
|
17 |
Дальн |
604 |
0,042 |
5800 |
35 |
=F2 |
=B17*E17 |
=C17*F17 |
=D17*G17 |
|
18 |
=СУММ (С2:С17) |
=СУММ(H2:H17) |
=СУММ(I2:I17) |
· Сервис - Поиск решения:
· Установить целевую ячейку I18 равной min;
· Изменяя ячейки E2:E17;
· Добавить ограничения Е2:Е17=Целое; Е2:Е17>=0; G2:G17>=H2:H17.
· После набора ограничений щелкаем ЛКМ по клавише «Выполнить». Этим самым производится запуск программы на оптимизацию. Результаты поиска отражаются в таблице.
·
Далее можно осуществлять оптимизацию при различных данных,
влияющих на значение целевой функции. При первом расчете можно положить ![]() .
.
· Не всегда решение может быть найдено. В этом случае можно щелкнуть ЛКМ по клавише «Параметры» и изменить предусмотренные там показатели: предельное число итераций; предельное время выполнения задачи; метод поиска и др.
Технология решения задачи распределения потребного объема ремонта вагонов по депо дороги
Задача решается также как и предыдущая задача. Отличие заключается лишь в содержании и формулах вычислений в некоторых ячейках. Так коэффициент долевого участия вагонных депо в проведении деповского ремонта вагонов в данной задаче вычисляется по формуле
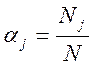 ,
,
где 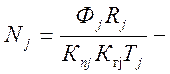 расчетный объем выпуска вагонов в
расчетный объем выпуска вагонов в ![]() м вагонном депо;
м вагонном депо;
![]() номинальный
годовой фонд рабочего времени в
номинальный
годовой фонд рабочего времени в ![]() м вагонном депо;
м вагонном депо;
![]() численность
рабочих в смене на вагоносборочном участке
численность
рабочих в смене на вагоносборочном участке ![]() го
депо;
го
депо;
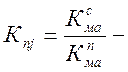 коэффициент
снижения трудоемкости работ при поточном методе по сравнению со стационарным
методом ремонта вагонов (
коэффициент
снижения трудоемкости работ при поточном методе по сравнению со стационарным
методом ремонта вагонов (![]() );
);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.