 в конкретном установившемся режиме. На рис.1.3
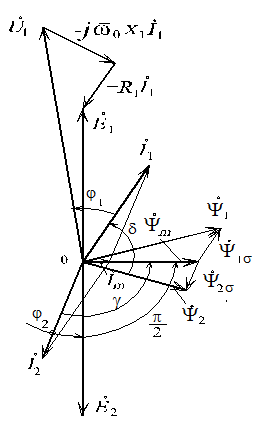
пред-ставлена векторная диаграмма для двигательного режима, на которой по оси
абсцисс направлены вектор намагничивающего тока
в конкретном установившемся режиме. На рис.1.3
пред-ставлена векторная диаграмма для двигательного режима, на которой по оси
абсцисс направлены вектор намагничивающего тока ![]() и совпадающий с
ним по фазе вектор потокосцепления от магнитного потока в зазоре
и совпадающий с
ним по фазе вектор потокосцепления от магнитного потока в зазоре ![]() . Потокосцепления статора
. Потокосцепления статора![]() и ротора
и ротора![]() отли-
чаются от потокосцепления
отли-
чаются от потокосцепления ![]() на величину
потокосце- плений от потоков рассеяния
на величину
потокосце- плений от потоков рассеяния ![]() и
и
![]() . Вектор ЭДС статора
. Вектор ЭДС статора ![]() сдвинут относительно
сдвинут относительно![]() на угол
на угол ![]() в
сторону опережения. ЭДС ротора определяется как
в
сторону опережения. ЭДС ротора определяется как ![]() =
=![]() . Вектор напряжения питания
. Вектор напряжения питания ![]() равен
сумме векторов ЭДС
равен
сумме векторов ЭДС ![]() и падений напряжений в
активном
и падений напряжений в
активном ![]() и индуктивном
и индуктивном![]() сопротивлениях
обмотки статора. Значения переменных определяются по схеме замещения и принятым
для расчета величинам фазного напряжения и частоты питания, а также
относительной частоте
сопротивлениях
обмотки статора. Значения переменных определяются по схеме замещения и принятым
для расчета величинам фазного напряжения и частоты питания, а также
относительной частоте ![]() роторной ЭДС, которая
Рис.1.3 Векторная диаграмма зависит от
нагрузки.
роторной ЭДС, которая
Рис.1.3 Векторная диаграмма зависит от
нагрузки.
Расчеты токов и потокосцеплений статора и ротора выполняются как для обычной схемы переменного тока по выражениям (1.3) ÷ (1.8) после замены в них индуктивностей на индуктивные сопротивления. Комплексные сопротивления равны, соответственно:
z1 = R1 + j x1
; z2 = R2/s+ j x2
; zm =
j xm.
Если обозначить через zЭ эквивалентное сопротивление
параллельного соединения сопротивлений zm
и z2, равное ![]() , то для тока и напряжения
первичного контура можно записать:
, то для тока и напряжения
первичного контура можно записать:
![]() ;
; ![]() , и окончательно:
, и окончательно: ![]() , (1.13)
, (1.13)
Схема замещения позволяет установить связи между
всеми переменными, рассчитать и построить необходимые зависимости. Наибольший
интерес представляет исследование характера изменения магнитного потока или
главного потокосцепления![]() при изменении
нагрузки и частоты питания, т.к. от
при изменении
нагрузки и частоты питания, т.к. от ![]() в значительной
степени зависит величина момента и всех других переменных двигателя. С
в значительной
степени зависит величина момента и всех других переменных двигателя. С ![]() напрямую связана ЭДС статора
напрямую связана ЭДС статора ![]() . Используя (1.13), с учетом
скорости изменений магнитного потока
. Используя (1.13), с учетом
скорости изменений магнитного потока ![]() ,
получим:
,
получим:
![]() ,
,
После подстановки в него выражений для полных сопротивлений z1 и zЭ получим:
 =
= ![]() (1.14)
(1.14)
где: ![]() .
.
Первый сомножитель – ![]() выражения (1.14) отражает смысл
основного закона частотного регулирования – необходимость пропорционального
изменения напряжения
выражения (1.14) отражает смысл
основного закона частотного регулирования – необходимость пропорционального
изменения напряжения ![]() при изменении частоты f. В этом случае обеспечивается (при принятых допущениях)
постоянство главного магнитного потокосцепления при идеальном холостом ходе,
т.к. при подстановке в (1.14) значения s = 0 имеем А =
1:
при изменении частоты f. В этом случае обеспечивается (при принятых допущениях)
постоянство главного магнитного потокосцепления при идеальном холостом ходе,
т.к. при подстановке в (1.14) значения s = 0 имеем А =
1:
![]() ,
(1.15)
,
(1.15)
Второй сомножитель – А характеризует
изменение ![]() при изменении частоты f и нагрузки, определяемой скольжением s.
при изменении частоты f и нагрузки, определяемой скольжением s.
По значениям потокосцепления ![]() рассчитывается ток
намагничивания:
рассчитывается ток
намагничивания:
![]() , (1.16)
, (1.16)
через который можно выразить и другие токи:
![]() ;
; ![]() , а затем после подстановки значений полных сопротивлений
получить их выражения:
, а затем после подстановки значений полных сопротивлений
получить их выражения:
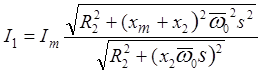 ,
(1.17)
,
(1.17)
![]() , (1.18)
, (1.18)
Для расчета активной составляющей тока ротора, необходимой для определения момента, используются выражения:
![]() ,
(1.19)
,
(1.19)
![]() , (1.20)
, (1.20)
Для определения момента можно воспользоваться одной из форм его представления:
![]() .
(1.21)
.
(1.21)
Так как расчеты выполнялись только для одной фазы, то коэффициент 3 отражает результирующее действие трех фаз.
Следует отметить тот факт, что напряжения на отдельных участках схемы замещения характеризуют соответствующие потокосцепления. Благодаря этому, легко установить взаимосвязь между потокосцеплениями и другими переменными. Так для потокосцепления ротора можно записать:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.