Колебательные процессы в тракторе. Структура низкочастотных динамических процессов в тракторе. Структурная схема САР угловой скорости вала двигателя, страница 5

∆М_вед=Р_к∆r_д.

Таким образом, колебания остова колесного трактора, так же как и гусеничного, могут вызывать изменения нагрузки на двигатель, угловой скорости коленчатого вала двигателя и скорости движения трактора независимо от колебаний силы тягового сопротивления вследствие изменения кинематического и динамического радиусов колеса.

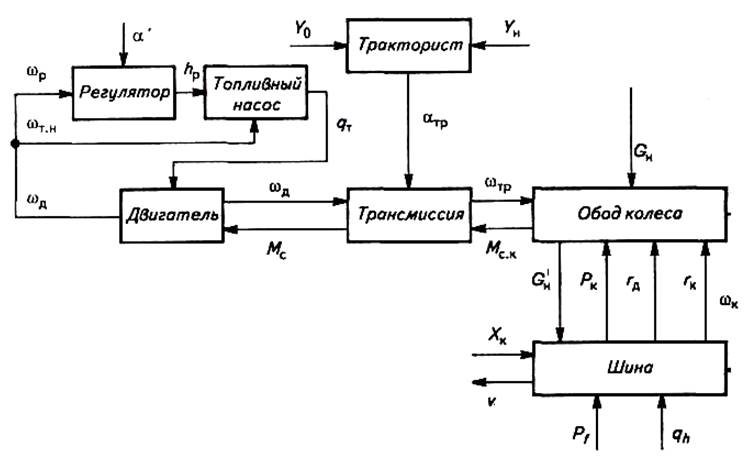
Рисунок 6.3 - Структурная схема колесного трактора как динамической системы

Структурная схема трактора как динамической системы (рис. 6.3) состоит из отдельных элементов, рассмотренных ранее.

Внешние воздействия на трактор как на динамическую систему включают: силу тягового сопротивления Р_кр, неровности профиля пути, по которому движется трактор и траекторию движения трактора, которую необходимо отслеживать. Главная выходная координата системы — действительная скорость поступательного движения трактора, ее колебания и снижение по сравнению с расчетной.

6.3. Показатели работы двигателя и трактора при колебаниях нагрузки

6.3.1. Недоиспользование мощности двигателя

Основоположник исследования работы тракторного двигателя при установившейся нагрузке академик В. Н. Болтинский отмечает, что из-за колебаний нагрузки происходит потеря мощности, так как колебания нагрузки и угловой скорости коленчатого вала отрицательно влияют на рабочий процесс двигателя, а также вызывают снижение коэффициентов наполнения и избытка воздуха, индикаторного и механического КПД.

Другие исследователи отмечают, что им не удалось получить экспериментально снижение энергетических и других показателей при работе двигателя на линейном участке регуляторной характеристики.

Рассмотрим схематически возможность влияния на среднее значение угловой скорости коленчатого вала двигателя только нелинейности регуляторной характеристики, полагая, что при этом отсутствуют другие факторы влияния на эффективную мощность двигателя.

Для упрощения и наглядности решения задачи предположим, что изменение момента сопротивления происходит по гармоническому закону с известной амплитудой ΔМ_с=ΔМ_к относительно среднего значения , соответствующего крутящему моменту двигателя в т. е М_ке (рис. 6.4). Амплитуде колебаний крутящего момента двигателя {+ΔМ_к+(-ΔМ_к)} соответствует амплитуда колебаний угловой скорости вала двигателя (ω₁-ω₂).

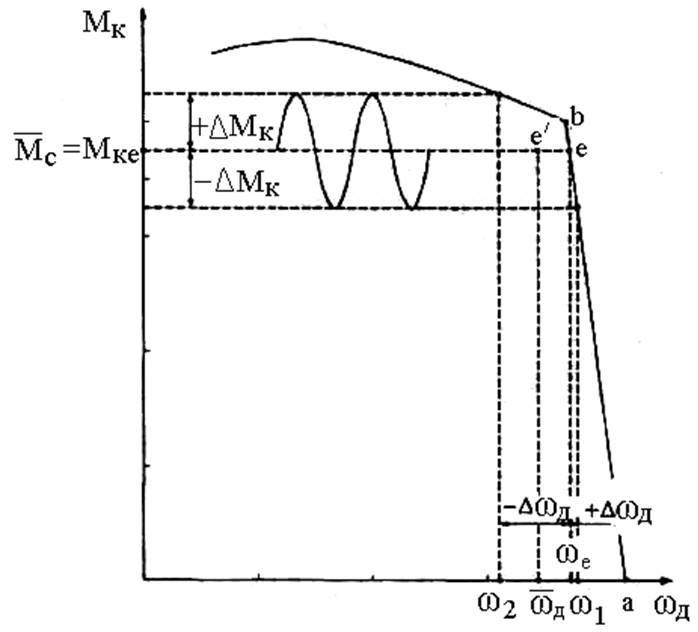
Рисунок 6.4 - Влияние колебаний нагрузки на снижение угловой скорости коленчатого вала двигателя по регуляторной характеристике

Условимся, что изменение крутящего момента двигателя и угловой скорости коленчатого вала при колебаниях нагрузки происходит строго по закону регуляторной характеристики, т. е. значения М_к и ω_д в любой момент времени соответствуют одной точке, всегда расположенной на кривой, выражающей статическую зависимость между этими параметрами.

При соблюдении этого условия и колебаниях момента в пределах ±ΔМ_К среднее за время опыта значение  будет находиться в т. е, что соответствует исходному положению. Угловая скорость коленчатого вала будет изменяться в пределах (ω₁-ω₂) с несимметричным отклонением от т. е: +Δω_д<-Δω_д. Это означает, что среднее за время опыта значение  (т. е' на рисунке 6.4) не будет равно угловой скорости коленчатого вала двигателя в т. е регуляторной характеристики.

Таким образом, несмотря на принятое условие, произошло "расслоение" характеристики, которое заключается в том, что одному и тому же значению  соответствуют разные значения частоты вращения коленчатого вала и, следовательно, разные значения эффективной мощности. Так как <ω_е, мощность при нагружении переменным моментом ниже, чем при нагружении постоянным моментом М_к:

.

Снижение мощности двигателя от неравномерной нагрузки в связи с принятой гипотезой (вследствие нелинейности регуляторной характеристики) следует объяснять недоиспользованием мощности, а не ее потерей. Уменьшение числа рабочих циклов (<ω_д) приводит к уменьшению часовой подачи топлива G_т, поэтому снижение индикаторной мощности N_i происходит даже при сохранении цикловой подачи и индикаторного КПД двигателя: