Использование основных положений теории информации для характеристики процесса измерений

8. использование основных положений теории информации для характеристики процесса измерений

Согласно теоремам Шеннона дезинформационное действие шума или помех при передаче сигнала определяется энтропией шума как случайной величины. Если шум в вероятностном смысле не зависит от передаваемого сигнала, то независимо от статистики сигнала шуму можно приписать определенную величину энтропии. Количество передаваемой информации I равно энтропии передаваемого сигнала за вычетом энтропии шума H(D).

I = H(Q)– H(D)

В случае измерения энтропия передаваемого сообщения H(Q) есть исходная или априорная энтропия измеряемой величины Q, определяемая лишь ее законом распределения p(Q). Энтропия шума в случае измерения  ‑ условная энтропия, характеризующая интервал неопределенности, оставшийся после выполнения измерения H(Q/Q_п.).

Происхождение этого термина объясняется следующим образом. Пусть в результате однократного измерения величины постоянного размера получаем показание Q_п. Учитывая класс точности средства измерений, мы можем лишь утверждать, что значение измеряемой величины находится где‑то в интервале Q_п ± k Q_п., где k – коэффициент, определяемый исходя из класса точности.

Представим ситуацию следующим образом. Имеются две системы U и V. Система U (объект) может принимать различные состояния в интервале от Q₁ до Q₂. Вместо непосредственного наблюдения за объектом (источником информации), ведется наблюдение за состоянием системы V (средство измерений), которая может принимать различные состояния в интервале от Q_min до Q_max. При получении показания Q_п средства измерения, имеющего ту же размерность, что и измеряемая величина, неопределенность, остающуюся после измерения, можно рассматривать как условную энтропию системы U (объекта) при условии, что система V (средство измерений) находится в состоянии Q_п. Тогда, согласно (4.2.), количество полученной информации

I = H(Q)– H(Q/Q_п.)                                           (8.1)

Результат передачи измерительной информации по каналу связи можно представить графически, как это показано на рис. 8.1. Вследствие воздействия целого ряда возмущающих факторов, показанию средства измерения Q_п может соответствовать целый ряд значений, которые с достаточным основанием могут быть приписаны измеряемой величине. На учитывая маловероятных случаев, такую ситуацию можно изобразить веером лучей, сходящихся в точке Q_п.

 

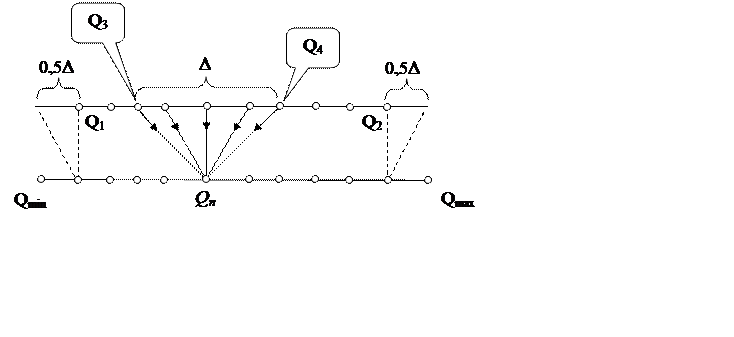Рис. 8.1. Графическая интерпретация неопределенности, остающейся после выполнения измерений

Неопределенность, обусловленная воздействием шума и помех и вносимая в процесс передачи измерительной информации, описывается условной энтропией H(Q/Q_п.).

Система V (средство измерений) является подчиненной по отношению к наблюдаемой системе U. В общем случае энтропия подчиненной системы меньше, чем энтропия той системы, которой она подчинена. Соответственно, максимальной количество информации, которое можно получить, в результате измерения, не превышает энтропии подчиненной системы. Поэтому, в самом крайнем случае необходимо обеспечить условие:

                                   Q₁ = Q_min;  Q₂ = Q_max .                                        (8.2)

Исключение краевых эффектов, связанных с передачей по каналу крайних значений Q₁ и Q₂ передаваемой величины Q, возможно только при условиях:

                     Q_min > Q₁ ‑ 0,5D,   Q_max < Q₂ + 0,5D                            (8.3)

Этот вывод полностью согласуется с одной из аксиом метрологии – без априорной информации измерений невозможно. Невозможен и выбор необходимого средства измерений. В дальнейшем, для упрощения изложения материала, будем полагать достаточным выполнение условия (8.2).

Пусть средство измерений имеет диапазон измерения от Q₁ до Q₂ , а в качестве априорной информации используются сведения о классе точности используемого средства измерений. При этом могут использоваться понятия абсолютной и относительной неопределенности.

Абсолютная неопределенность, остающаяся после выполнения измерений и не зависящая от текущего значения Q , характеризуется пределами, в которых может находиться значение величины, поданной на вход средства измерений, и значением полу суммы этих пределов:

                                      Q₄ – Q₃ = D;    Q_п. = 0,5(Q₄ + Q₃)                              (8.4)

Приведенная относительная неопределенность характеризуется величиной

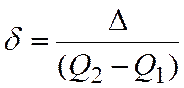                                                                          (8.5)

В теории информации тот факт, что средство измерений имеет диапазон измерений от Q₁ до Q₂, означает, что при его использовании могут быть получены показания Q_п только в пределах от Q₁ до Q₂. Вероятность получения отсчетов, меньших Q₁и больших Q₂ равна нулю. Вероятность получения отсчетов в пределах от Q₁ до Q₂ равна единице. Если предположить, что плотность распределения вероятности значений измеряемой величины вдоль шкалы средства измерений одинакова, то с точки зрения теории информации наше знание о значении измеряемой величины до измерения может быть представлено графиком распределения плотности вероятности p(Q) вдоль шкалы значений, показанным на рис. 8.2.

Так как полная вероятность получить отсчет в пределах от Q₁ до Q₂ равна единице, то под кривой p(Q) должна быть заключена площадь, равная единице (условие нормирования). При равномерном распределении плотности вероятности это приводит к выражению

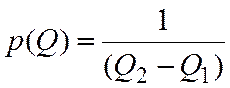
После проведения измерения получаем показание прибора, равное Q_п. Однако, вследствие воздействия помех и шумов, мы не можем утверждать, что измеряемая величина, поданная на вход средства измерений, точно равна Q_п. . Поэтому записываем результат измерения в виде

Q_п – 0,5D £ Q £ Q_п + 0,5D

 

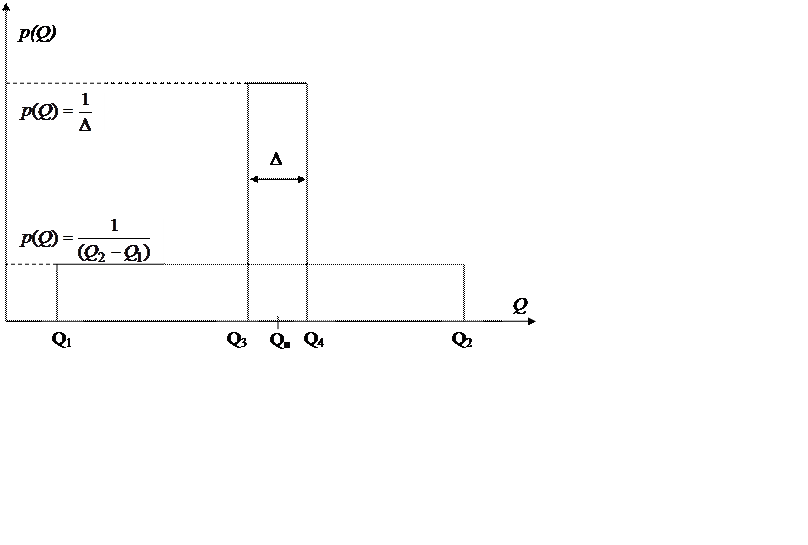Рис. 8.2. график плотности распределения вероятности до и после измерения.

Значение измеряемой величины постоянного размера находится в пределах интервала D. С точки зрения теории информации результат измерения состоит лишь в том, что до измерения область неопределенности простиралась от Q₁ до Q₂ и характеризовалась малой плотностью вероятности p(Q)=1/(Q₁– Q₂) , а после измерения она сократилась до величины D и характеризуется намного большей плотностью вероятности p(Q)=1/(D ).

Получение информации об интересующей нас величине заключается, таким образом, в уменьшении неопределенности ее значения. Формальный прием для математической записи этого логического заключения состоит в определении количества информации I как уменьшения энтропии от значения H(Q) , которое характеризует неопределенность измеряемой величины перед измерением, до значения H(Q/Q_п.) , которое остается после получения показания средства измерения Q_п., т.е. согласно выражению (8.1.).